Содержание
Описание и примеры стандартных функций SVG
Доминирующей причиной появления этого блога стало незаслуженное забвение на целых десять лет языка разметки масштабируемой векторной графики – SVG (Scalable Vector Graphics), входящего в подмножество расширяемого языка разметки XML.
Стандарт SVG 1.0 был принят в качестве спецификации Консорциумом Всемирной паутины (W3C) в сентябре 2001 г. Стандарт SVG 1.1 и его версии SVG mobile profiles (SVG Basic and SVG Tiny) были приняты консорциумом в качестве рекомендации в январе 2003 г.
Сейчас ведутся работы по созданию стандарта SVG 2.0
Основные преимущества формата SVG.
Я не буду долго распространяться о преимуществах векторной графики перед растровой в вебдизайне, замечу лишь, что, однажды созданный, файл в формате SVG одинаково хорошо выглядит без потери качества и на мобильном устройстве и на станционарном мониторе домашнего ПК.
Шапка данного сайта выполнена в формате SVG, попробуйте уменьшить окно браузера до минимальных размеров, картинка на “лету” будет также пропорционально уменьшаться.
SVG – это двухмерная графика и тем не менее это текстовый формат, который можно легко править в блокноте или просто рисовать в векторных редакторах: Incscape , Adobe illustrator, CorelDRAW
Бесконечное полотно документа svg.
Итак, как происходит формирование векторного изображения.
Документ формата SVG – это двухмерный объект, который может иметь бесконечные координаты, как в положительном, так и в отрицательном направлении по осям X и Y. Также документ SVG имеет две области просмотра: viewport – системная область просмотра и viewBox – пользовательская область просмотра, положение которой относительно начала системных координат viewport, может задаваться собственной, пользовательской системой координат. Другими словами окно просмотра viewBox, может быть перемещёно в любое место документа SVG, при этом берется фрагмент изображения под ним, который после процесса согласования между viewBox и viewport, возвращается обратно в системную область просмотра viewport, которую видит пользователь.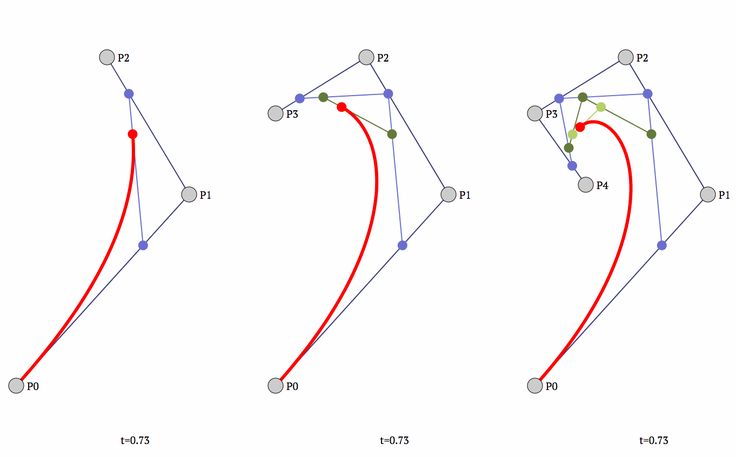 Используя это свойство можно организовать вертикальную или горизонтальную прокрутку изображения, меняя параметры координат viewBox.
Используя это свойство можно организовать вертикальную или горизонтальную прокрутку изображения, меняя параметры координат viewBox.
При уменьшении размера пользовательского окна просмотра viewbox можно пропорционально увеличивать фрагмент изображения в системной области просмотра или уменьшать его при увеличении размера viewbox.
Таким образом реализуется эффект лупы. Более подробно эти процессы разобраны в статье: Трансформация изображений SVG при изменении параметров Viewbox.
Взаимодействие SVG, XML с HTML, CSS, Jscript
В SVG, как и в HTML можно добавлять ссылки на внешние ресурсы. Но если в HTML одна картинка может служить только для одной внешней ссылки, то в SVG документ можно добавлять сколько угодно внешних ссылок . Картинка кликабельна.
Внутрь HTML страницы легко встраивается код SVG документа или целиком подключается внешний SVG файл. Можно наоборот, внутри SVG файла разместить код HTML внутри тегов foreignObject. Получаются интересные эффекты: Внутри SVG файла находится работающий внешний HTML сайт.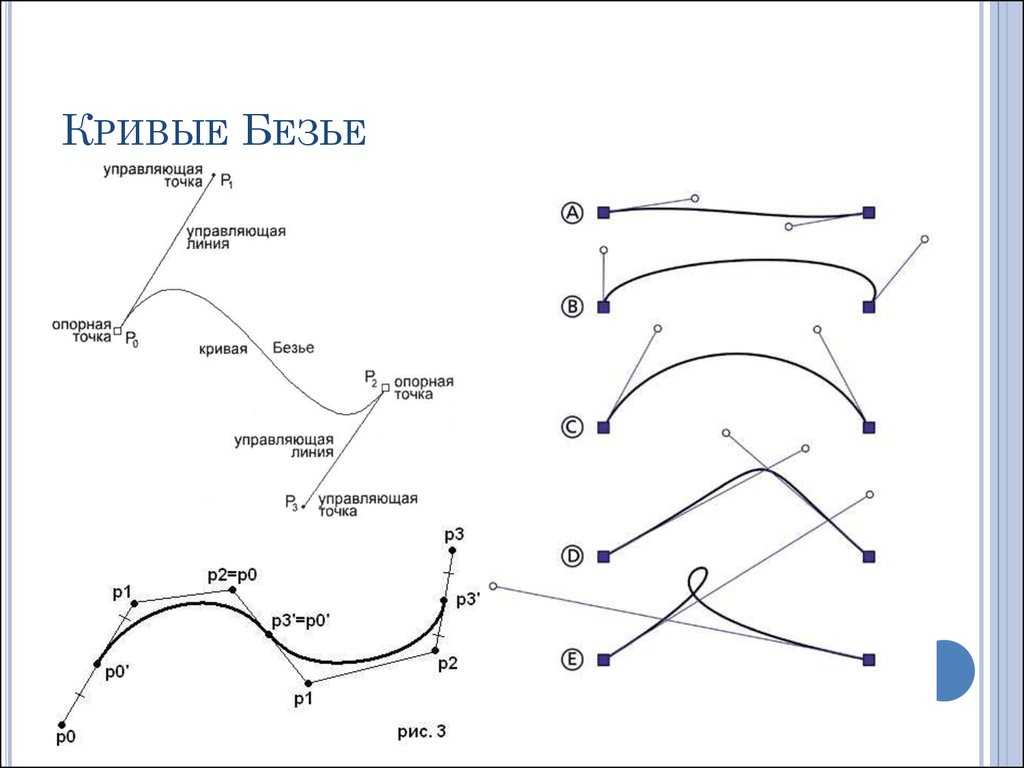 К SVG формату можно подключать внешние таблицы стилей CSS 2.0, что позволяет управлять сразу несколькими файлами *.svg. Также вполне допустимо подключение стилей внутри файла *.svg внутри тегов style или использовать внутренние стили непосредственно внутри командных строк фигур и путей.
К SVG формату можно подключать внешние таблицы стилей CSS 2.0, что позволяет управлять сразу несколькими файлами *.svg. Также вполне допустимо подключение стилей внутри файла *.svg внутри тегов style или использовать внутренние стили непосредственно внутри командных строк фигур и путей.
SVG, как любой основанный на XML формат, позволяет использовать для его обработки таблицы трансформации (XSLT).
Преобразуя XML-данные в SVG с помощью простого XSL, можно получить графическое представление текстовых данных, например визуализировать графики, круговые диаграммы, гистограммы и т.д.
Анимация и интерактивность SVG.
Анимация в SVG осуществляется при помощи языка SMIL (Synchronized Multimedia Integration Language). Также поддерживаются скриптовые языки на основе спецификации ECMAScript — это встраиваемый расширяемый язык программирования.
То есть всё находится в одном месте, внутри документа SVG, поэтому нет необходимости для подключения внешних библиотек.
На каждую отдельную фигуру или на целое изображение можно установить обработчик событий (клик, наведение мышки, нажатие клавиши и т.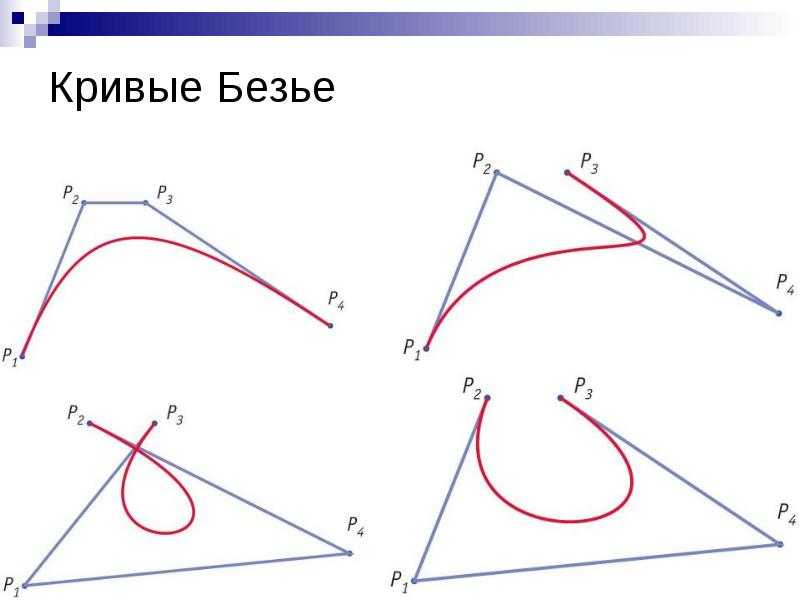 д), таким образом, пользователь может управлять рисунком. Наведите курсор мышки на кнопку“Start” на примере слева.
д), таким образом, пользователь может управлять рисунком. Наведите курсор мышки на кнопку“Start” на примере слева.
По событию mouseover на этой кнопке начнется анимация по команде begin=”startButton.mouseover” – движение цветных шариков по криволинейному пути. Закончится анимация либо через заданные в коде 16 секунд, либо в любой момент по наведению курсора мышки на цветные радиокнопки “Stop”. При этом каждая радиокнопка управляет своим объектом совпадающим по цвету. На рисунке ниже анимация начинается и заканчивается при нажатии клавиши мышки на кнопки GO и STOP. В этом случае работает событие click. Команда на запуск анимации – begin=”gO.click” и соответственно остановка – end=”stop.click”
Следующий пример анимации – плавная отрисовка картинки с нуля до полного изображения.
Уже встроенные в SVG языки программирования позволяют реализовать довольно сложные сценарии анимации. Но, в дополнение к этому есть еще более мощные средства для реализации интерактивности графики и ее анимации – это внешние библиотеки сторонних разработчиков: D3.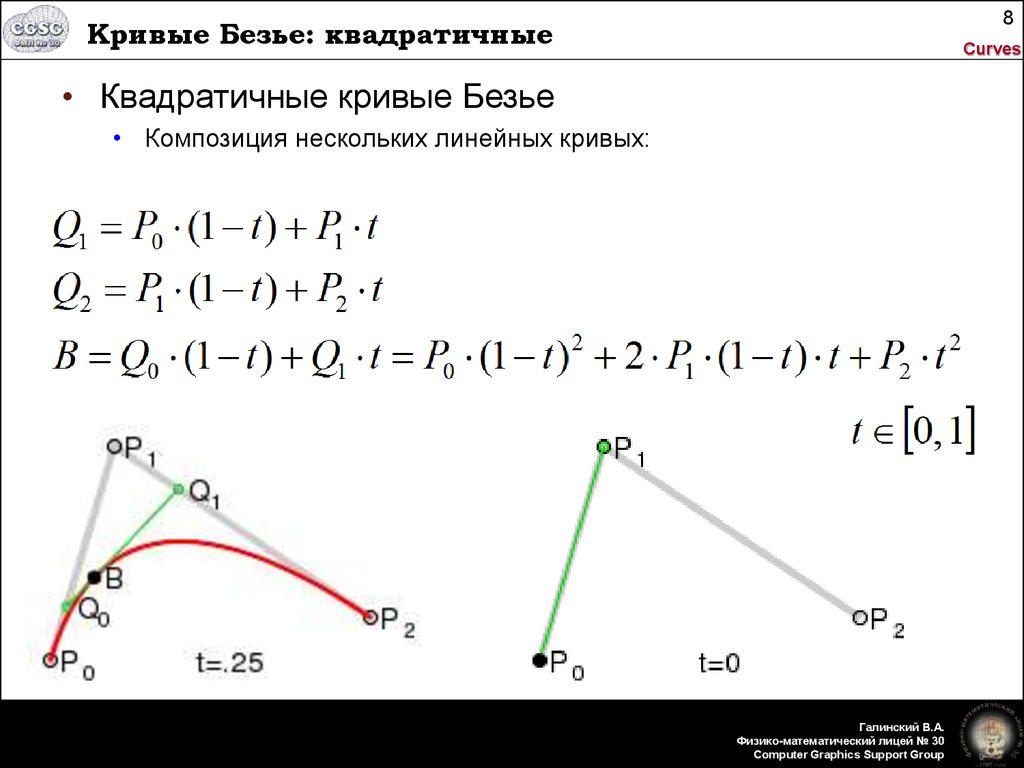 js, BonsaiJS, Svg.js, Snapsvg.js
js, BonsaiJS, Svg.js, Snapsvg.js
Еще примеры анимации ⇛
Недостатки SVG формата
- С увеличением количества мелких деталей в изображении, быстрее растёт размер файла SVG-данных. Предельный случай — когда изображение представляет собой белый шум. В этом случае SVG не только не даёт никаких преимуществ в размере файла, но даже имеет проигрыш по отношению к растровому формату. На практике, SVG становится невыгоден уже задолго до того, как изображение дойдёт до стадии белого шума.
- Трудность использования в крупных картографических приложениях из-за того, что для правильного отображения маленькой части изображения документ необходимо прочитать целиком.
- В настоящее время SVG формат применяется в Интернете сравнительно мало, из-за недостаточной кроссбраузерности. Лучше всего обстоят дела у Mozilla Firefox со встроенным просмотрщиком SVG, так как ее разработчики находятся в рабочей группе Консорциума Всемирной паутины (W3C) по разработке и внедрению стандарта SVG.
 Хуже всего дела по поддержке формата SVG у Microsoft, которая покинула группу 2003 г. Для Internet Explorer – необходим Adobe SVG Viewer (ASV). С 9 версии IE частично поддерживает функции SVG.
Хуже всего дела по поддержке формата SVG у Microsoft, которая покинула группу 2003 г. Для Internet Explorer – необходим Adobe SVG Viewer (ASV). С 9 версии IE частично поддерживает функции SVG.
Браузеры Apple Safari, Google Chrome намного лучше поддерживают SVG, но не полностью, так как SVG – это большая спецификация (вдвое больше HTML 4.01), именно поэтому разработчики браузеров внедряют функции постепенно, от версии к версии. Но абсолютно все разработчики современных браузеров заявляют, что за форматом SVG будущее в области графики вебдизайна.
UPD. Добавлен новый раздел онлайн генераторы SVG кода path.
следующая: Структура SVG документа ⇛
Математические основы машинной графики
Математические основы машинной графики
Оглавление
|
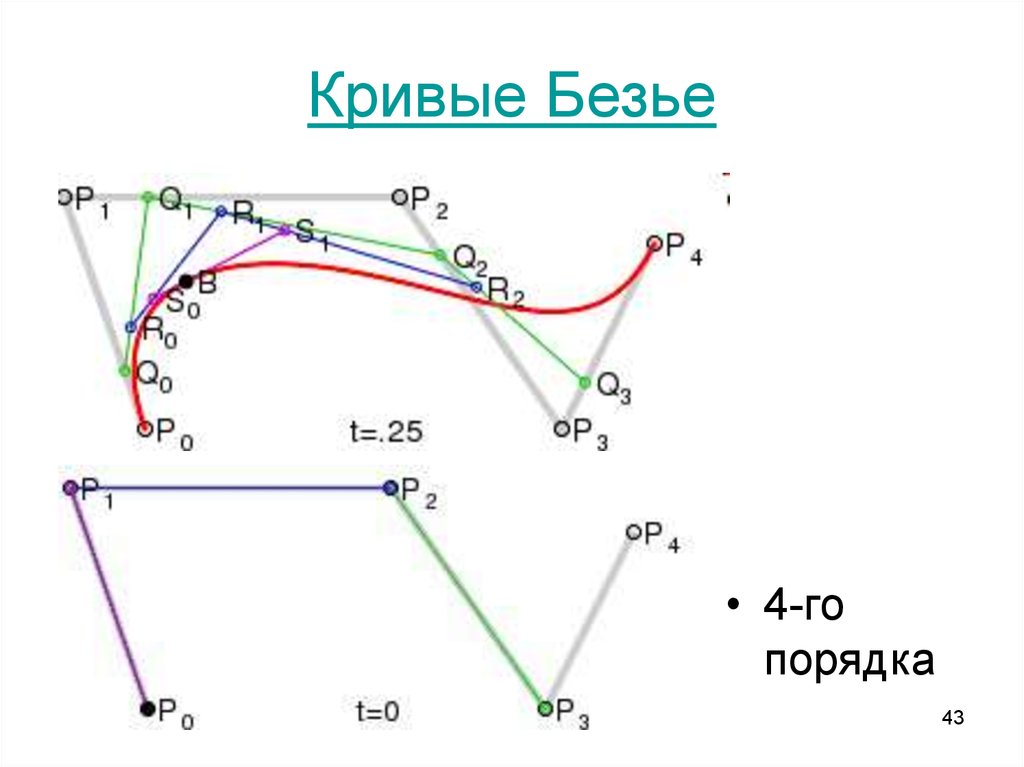
Кривая Безье.
 Поймите математику Безье… | by Omar Aflak
Поймите математику Безье… | by Omar Aflak
Понимание математики кривых Безье
Кривые Безье широко используются в компьютерной графике, часто для создания плавных кривых, и тем не менее они являются очень простым инструментом. Если вы когда-либо использовали Photoshop, вы могли наткнуться на инструмент под названием «Якорь», где вы можете ставить опорные точки и рисовать с их помощью какие-то кривые… Да, это кривые Безье. Или, если вы использовали векторную графику, SVG, они тоже используют кривые Безье. Посмотрим, как это работает.
Дано n+1 точек (P0, …, Pn) называется контрольных точек , кривая Безье, определяемая этими точками, определяется как:
экв. 1
Где B(t) — полином Бернштейна, а:
экв. 2
Вы заметите, что этот многочлен Бернштейна очень похож на член k(th) в биномиальной формуле Ньютона:
экв.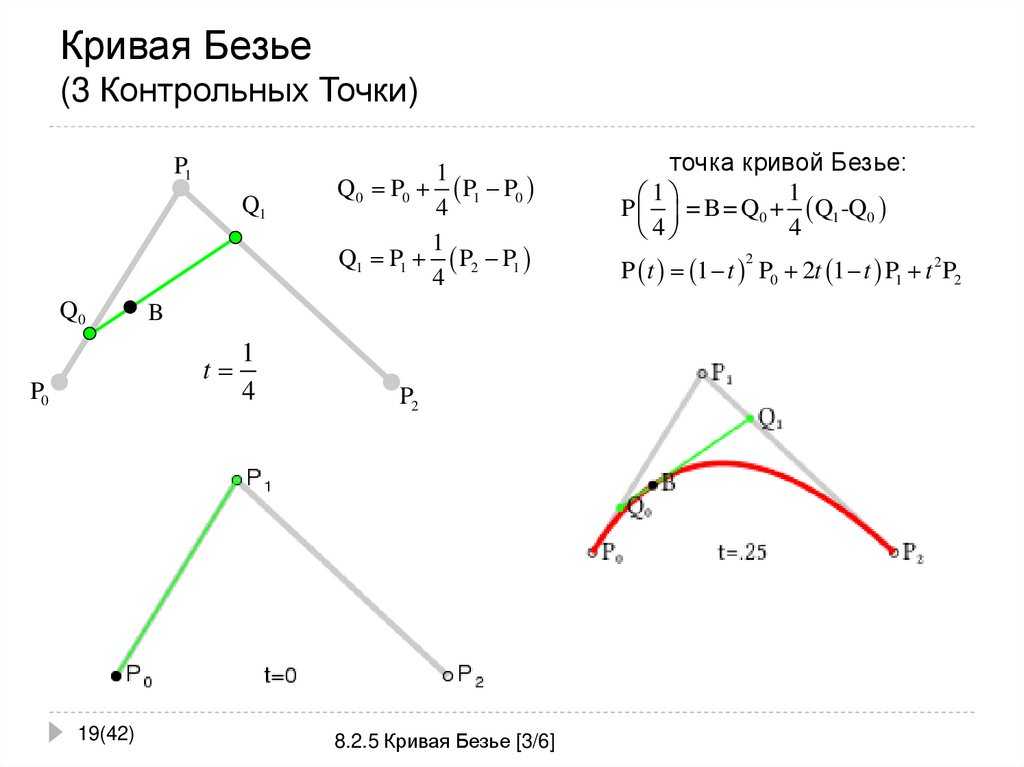 3
3
На самом деле многочлен Бернштейна есть не что иное, как 9n = 1. Вот почему, если вы суммируете все Bi до n , вы получите 1 . В любом случае.
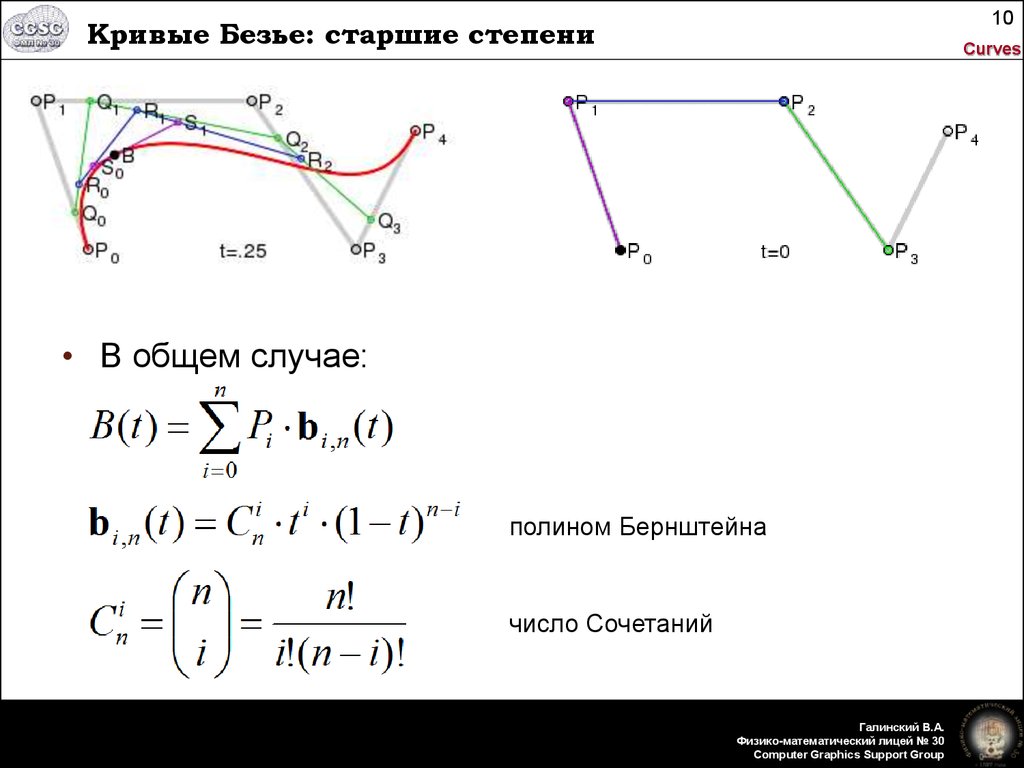
Квадратичная кривая Безье — это то, как мы называем кривую Безье с 3 контрольными точками, поскольку степень P(t) будет равна 2. Давайте рассчитаем кривую Безье с учетом 3 контрольных точек и исследуем некоторые свойства, которые мы можем найти! Помните, экв. 1 соответствует n+1 точек, поэтому в нашем случае n=2.
экв. 4
Имейте в виду, что P(t) возвращает не число, а точку на кривой. Теперь нам осталось выбрать три контрольные точки и оценить кривую в диапазоне [0, 1] . Мы можем сделать это в Python довольно легко.
Вы можете заметить, что кривая начинается и заканчивается в первой и последней контрольных точках. Этот результат будет верным для любого количества точек. Поскольку t находится в диапазоне от 0 до 1 , мы можем доказать это, оценив P(t) в
Этот результат будет верным для любого количества точек. Поскольку t находится в диапазоне от 0 до 1 , мы можем доказать это, оценив P(t) в t=0 и t=1 . Используя экв. 1 :
экв. 4 экв. 5
Поскольку кривая идет от P0 до P2 , в этом случае P1 целиком определяет форму кривой 900 10 . Перемещаясь P1 вокруг вы можете кое-что заметить:
Кривая Безье всегда содержится в многоугольнике, образованном контрольными точками. Этот многоугольник поэтому называется контрольный многоугольник , или многоугольник Безье. Это свойство также сохраняется для любого количества контрольных точек, что делает управление ими интуитивно понятным при использовании программного обеспечения.
На самом деле мы можем представить формулу Безье, используя умножение матриц, что может быть полезно в других случаях, например, для разделения кривой Безье. Если мы вернемся к нашему примеру, мы можем переписать P(t) следующим образом:
Если мы вернемся к нашему примеру, мы можем переписать P(t) следующим образом:
экв. 6
Итак, вся информация о квадратичной кривой Безье сжата в одну матрицу, М . Теперь мы можем захотеть найти коэффициенты этой матрицы, не выполняя все эти шаги и легко программируемым способом. Поскольку коэффициенты матрицы — это просто коэффициенты полинома перед каждым Pi , то, что мы ищем, — это расширенная форма полинома Бернштейна экв. 2 .
Еще одна вещь: если мы расширим Bi(t) , мы получим многочлен перед Pi , что соответствует i(му) столбцу в матрице. Однако это не очень удобно, и было бы проще программировать, если бы вместо этого мы могли получать строки. Тем не менее, вы можете заметить, что i (я) строка матрицы точно такая же, как перевернутый (n-i) (th) столбец , и коэффициенты перевернутого (n-i) (th) столбца есть не что иное, как коэффициенты B(n-i)(t) , взятые в убывающей степени t .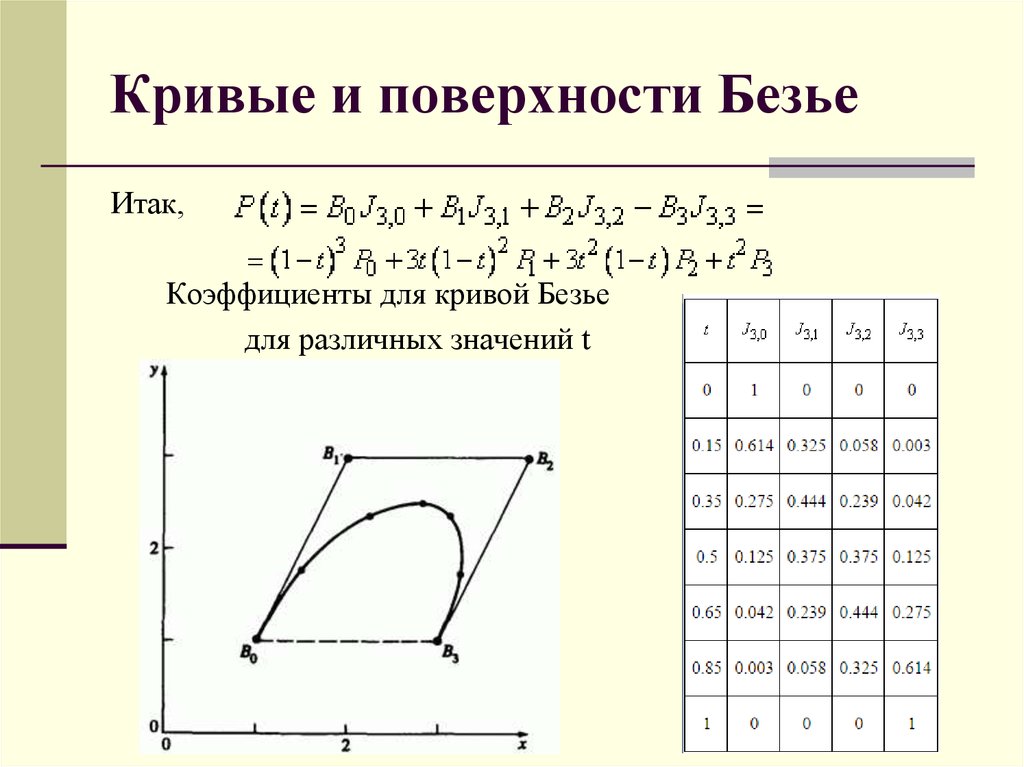
экв. 7
Вы можете обратиться к экв. 2 и экв. 3 , если у вас возникли проблемы.
Следовательно, коэффициенты матрицы есть не что иное, как коэффициенты перед t , что означает:
экв. 8
Одним из интересных применений кривых Безье является рисование гладкой кривой, проходящей через заданный набор точек. Это интересно потому, что формула P(t) дает точек и не имеет формы y=f(x) , поэтому одно x может иметь несколько y (в основном функция, которая может «идти назад»). Например, мы могли бы нарисовать что-то вроде этого:
Однако математика для получения этого результата нетривиальна, поэтому я написал для этого специальный пост:
Интерполяция Безье
Создание гладких форм с помощью кривых Безье.
по направлению datascience.com
А пока вот как можно запрограммировать общую версию кривой Безье для любого количества контрольных точек, используя экв. . 1
1
Запустите программу, и вы получите график, отображаемый в заголовке.
Это введение в кривые Безье. Я надеюсь, что вы узнали что-то новое, и не стесняйтесь комментировать любой вопрос, который у вас может возникнуть!
Что такое кривые Безье в компьютерной графике?
Кривые Безье могут многое. Вы можете использовать их для рисования фигур и шаблонов дизайна, например. Их также можно использовать математически вместо линейного представления изменений, постепенно и тонко переключаясь между одним ключевым кадром или значением и другим позже.
Вы можете узнать это приложение в анимационных программах, таких как Adobe Animate, но использование кривых Безье выходит далеко за рамки мира искусства.
В этом простом объяснении мы собираемся отложить численный анализ в пользу чего-то более подходящего для наших нужд, например, использования кривых Безье в творческих приложениях, таких как Photoshop и After Effects. Что же делает их такими замечательными?
Что такое кривая Безье?
Кривые Безье, основанные на концепции математики, называемой полиномом Бернштейна, были изобретены французским инженером Пьером Безье.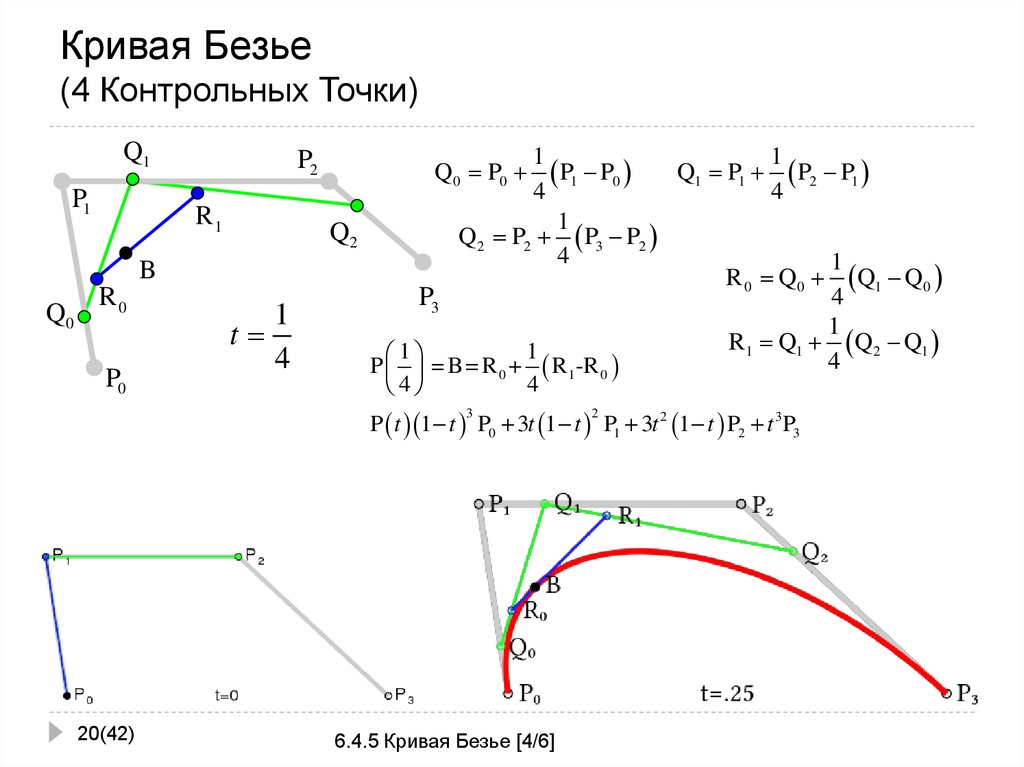 С тех пор кривые Безье превратились в предпочтительное решение для дизайнеров, которым нужен способ добраться из точки А в точку Б наиболее эстетичным способом.
С тех пор кривые Безье превратились в предпочтительное решение для дизайнеров, которым нужен способ добраться из точки А в точку Б наиболее эстетичным способом.
Кривые Безье генерируются с помощью алгоритма, управляемого последовательностью контрольных точек, выраженной в терминах n + 1. Этот алгоритм особенно подходит для разделения промежуточного пространства, оценки и дифференциации каждой прогрессивной точки в желаемой градуирующей кривой.
Кривые Безье являются векторами по своей природе — в отличие от растровых растровых кривых, они масштабируемы, что означает, что они сохраняют определенные свойства при увеличении или уменьшении их масштаба.
Где найти кривые Безье?
Кривые Безье распространены не только в пакете Adobe (в таких приложениях для творчества, как Premiere, Photoshop и After Effects), но вы найдете их практически в любом приложении для творчества.
Приложения для создания визуальных медиа, вероятно, первое, что приходит на ум, но давайте не будем забывать о приложениях для аудиоинженерии, таких как Pro Tools, где кривые Безье могут использоваться для изменения активов по параметрам или во времени.
Несколько распространенных примеров кривых Безье в дикой природе:
- Инструмент «Перо» в программах векторного дизайна Photoshop и , таких как Adobe Illustrator (и практически в любом другом приложении для творчества, в пакете Adobe и где угодно еще).
- Любое приложение, в котором используются кривые ключевых кадров Easy In / Easy Out , например After Effects .
- Всякий раз, когда вы имеете дело с NURBS , также известными как B-сплайны, в приложении для 3D-анимации или моделирования, таком как Maya или Blender , вы работаете с кривыми Безье в массовом порядке.
- Приложения САПР или любой другой цифровой инструмент, используемый для проектирования, также используют кривые Безье для многих целей.
Кривые Безье скрываются повсюду, вокруг нас. Как именно эти вещи делают то, что они делают?
Связано: Как создать или отредактировать узор в Adobe Illustrator
Как работают кривые Безье?
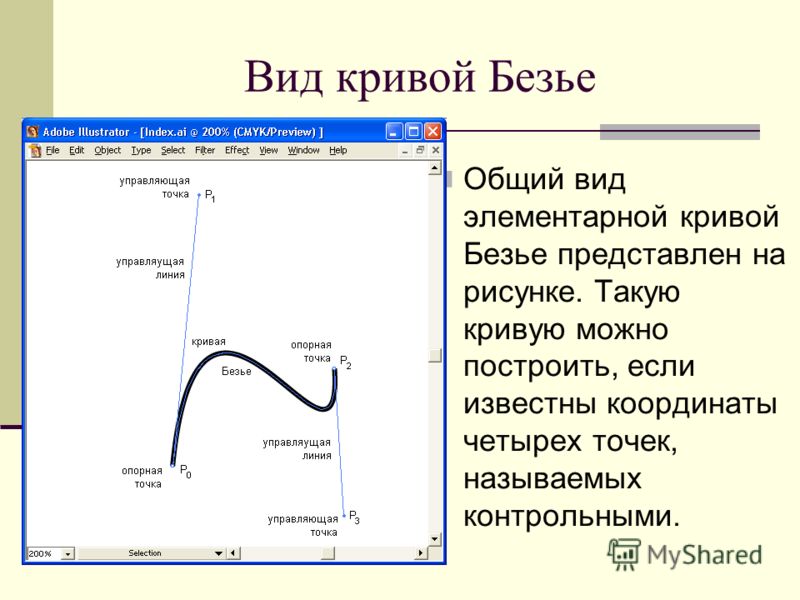
При создании нового вектора кривой Безье на холсте в таком приложении, как Illustrator, вы обычно начинаете с того, что даете программе две точки для работы; первая точка и вторая, с натянутой между ними кривой.
Квадратичная кривая Безье — это любая кривая Безье, созданная с использованием только этих двух начальных точек — кубические кривые Безье состоят из трех и так далее. Сейчас мы сосредоточимся на первом; самые простые из возможных кривых Безье, которые вы можете создать в любом из упомянутых нами типов программного обеспечения.
Обычно вы указываете приложению создать кривую Безье вместо линейного вектора, удерживая мышь и перетаскивая кривую на место, прежде чем отпустить вторую точку; после отпускания у вас будет два маркера интерполяции для каждой точки, составляющей кривую, включая любые дополнительные точки, которые вы записали постфактум.
От чего зависит, как будет выглядеть ваша кривая Безье?
- Расположение двух ваших точек, включая их «высоту» относительно друг друга и расстояние между ними.
- Интерполяция манипуляторов, найденных в каждой точке — вы используете эти манипуляторы, чтобы «направлять» кривую, изгибая ее на место.
- Пункты управления; «воображаемые» точки, найденные на пике линейной интерпретации как положения, так и интегрального шага вашей начальной и конечной точек (эта часть имеет больше общего с математикой, чем кривые Безье, в практическом, творческом смысле, но это все еще очень реально)
Как выглядят эти контрольные точки?
Представьте себе две прямые линии, направленные внутрь друг друга из любой крайней точки, просто взглянув на внешний край каждой стороны кривой.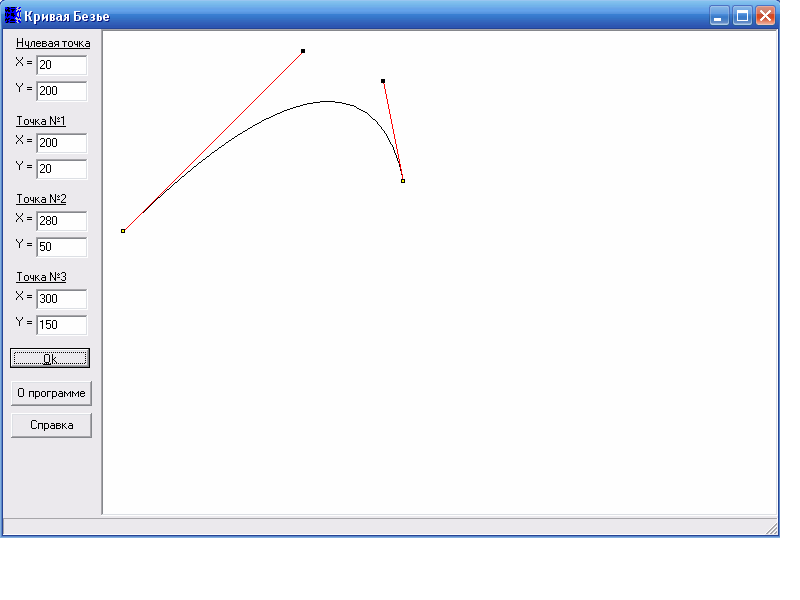 Точка, в которой эти две линии пересекаются посередине, будет «контрольной точкой» математически любой квадратичной кривой Безье, несмотря на то, что ни один набор маркеров интерполяции не обязательно связан с ней напрямую.
Точка, в которой эти две линии пересекаются посередине, будет «контрольной точкой» математически любой квадратичной кривой Безье, несмотря на то, что ни один набор маркеров интерполяции не обязательно связан с ней напрямую.
Связанный: Как векторизовать изображение в Adobe Illustrator
После того, как вы уже разложили перед собой кривую, вы можете использовать ручки, чтобы изменить ее траекторию по желанию. Кривые Безье связаны по определению, поэтому их можно использовать для элегантного и идеально сбалансированного соединения любых двух точек на конечном поле.
Процесс создания кривой Безье прост и интуитивно понятен; так легко увидеть, как этот тип инструмента достиг вездесущности, которой он пользуется в настоящее время.
Применение кривой Безье за пределами среды
Кривые Безье можно использовать для создания собственных оригинальных рисунков или для отслеживания существующих форм, изображений и композиций. Они часто широко используются в векторной 2D-анимации, например, как часть процесса очистки.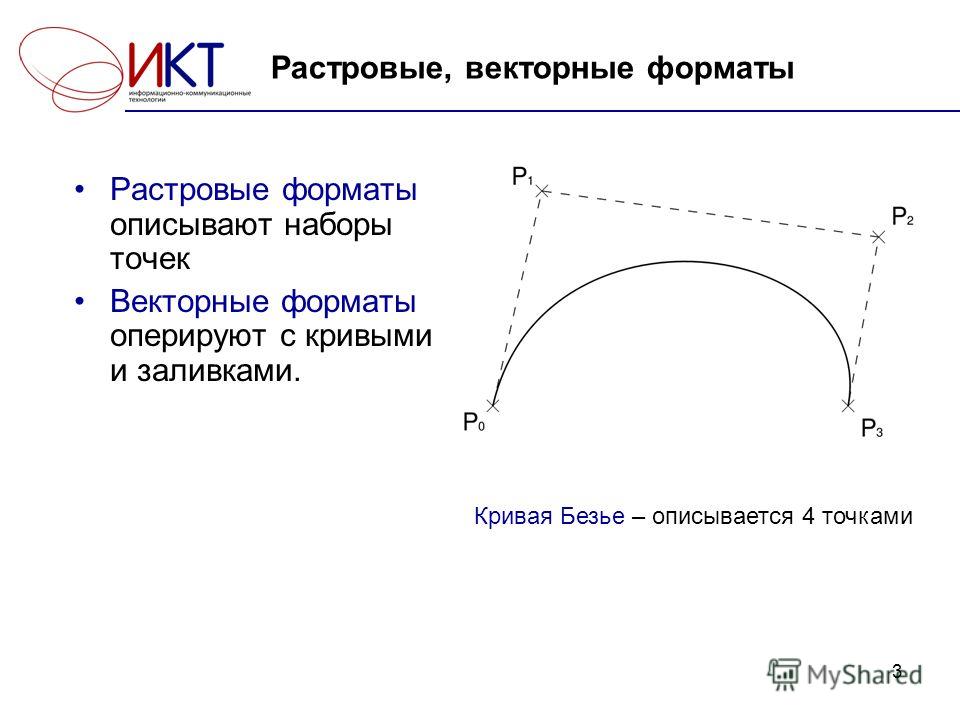
Хотя художники всего мира, безусловно, взяли эту концепцию и перетряхнули ее, ее математические корни делают ее чрезвычайно полезной и в ряде других профессий и дисциплин.
Кривые Безье могут применяться не только в искусстве и дизайне, но и в других сферах:
- Архитектура и строительство, например, при проектировании супермагистралей.
- Промышленный дизайн, включая дизайн игрушек, мебели и автомобилей.
- Робототехника. Кривые Безье могут помочь в компьютеризированной локомоции и картировании местности.
- 3D-сканирование в биомедицинском контексте, когда цифровой объект создается из множества 2D-сечений реального объекта (например, таких вещей, как компьютерная томография).
Это не говоря уже о ценности кривых Безье для интеллектуальных способностей, поскольку они стоят среди всего остального, что человечество знает о математике и истинной природе реальности в общем смысле. Это хардкорный материал, и временами абсолютно ужасающий.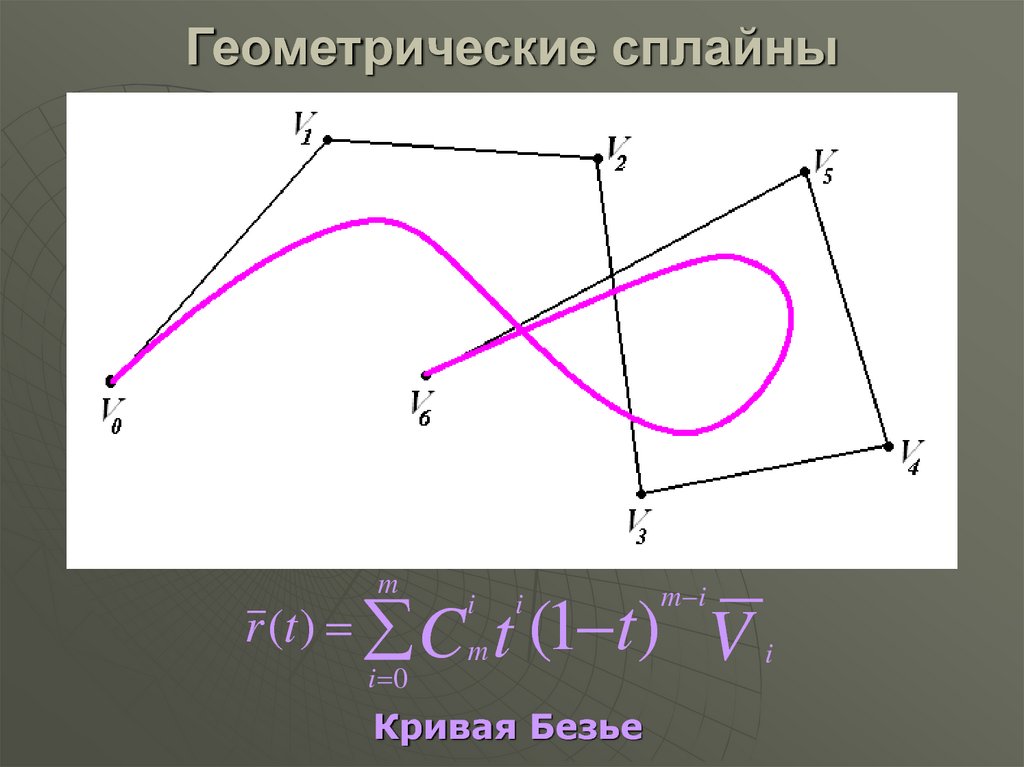

 Хуже всего дела по поддержке формата SVG у Microsoft, которая покинула группу 2003 г. Для Internet Explorer – необходим Adobe SVG Viewer (ASV). С 9 версии IE частично поддерживает функции SVG.
Хуже всего дела по поддержке формата SVG у Microsoft, которая покинула группу 2003 г. Для Internet Explorer – необходим Adobe SVG Viewer (ASV). С 9 версии IE частично поддерживает функции SVG.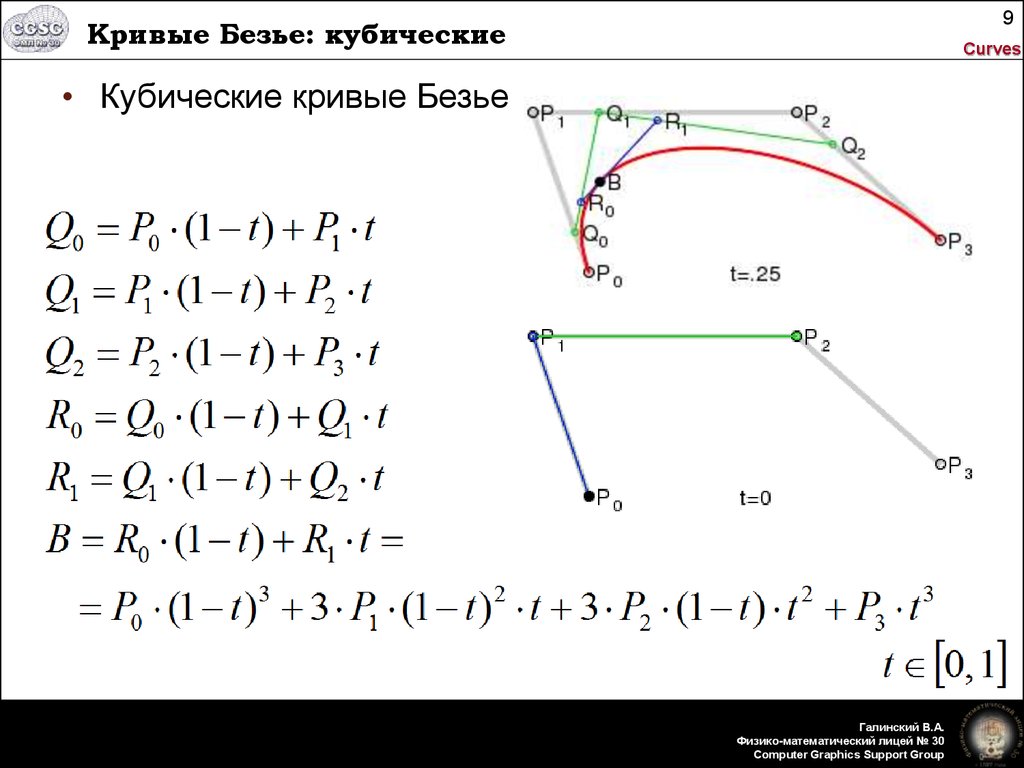 , Адамс Дж. Математические основы машинной графики. М.: Мир, 2001. 604 с.
, Адамс Дж. Математические основы машинной графики. М.: Мир, 2001. 604 с.
 Двумерные преобразования
Двумерные преобразования