Выпуклая линия: Построение минимальных выпуклых оболочек / Хабр

Построение минимальных выпуклых оболочек / Хабр


Проведя небольшое научное исследование (проще говоря, выполнив поиск на сайте), обнаружил, что на хабре имеется всего две статьи с тегом

вычислительная геометрия

, причем одна из них оказалась моей. Т.к. в последнее время я несколько заинтересовался этой тематикой, то решил продолжить тему алгоритмической геометрии рассмотрением задачи построения так называемых минимальных выпуклых оболочек. Хотя рисунок справа и дает проницательному хаброчитателю исчерпывающее объяснение того, что это такое, тем не менее под катом будут даны чуть более формальные определения и описаны два классических алгоритма построения минимальных выпуклых оболочек.


Пусть на плоскости задано конечное множество точек A. Оболочкой этого множества называется любая замкнутая линия H без самопересечений такая, что все точки из A лежат внутри этой кривой. Если кривая H является выпуклой (например, любая касательная к этой кривой не пересекает ее больше ни в одной точке), то соответствующая оболочка также называется выпуклой. Наконец, минимальной выпуклой оболочкой (далее кратко МВО) называется выпуклая оболочка минимальной длины (минимального периметра). Я не проверял (похоже, это можно доказать от противного), но кажется очевидным, что минимальная оболочка просто обязана быть выпуклой. Все введенные понятия иллюстрируются следующим рисунком.


Главной особенностью МВО множества точек A является то, что эта оболочка представляет собой выпуклый многоугольник, вершинами которого являются некоторые точки из A. Поэтому задача поиска МВО в конечном итоге сводится к отбору и упорядочиванию нужных точек из A. Упорядочивание является необходимым по той причине, что выходом алгоритма должен быть многоугольник, т.е. последовательность вершин. Наложим дополнительно условие на порядок расположения вершин — направление обхода многоугольника должно быть положительным (напомню, что положительным называется обход фигуры против часовой стрелки).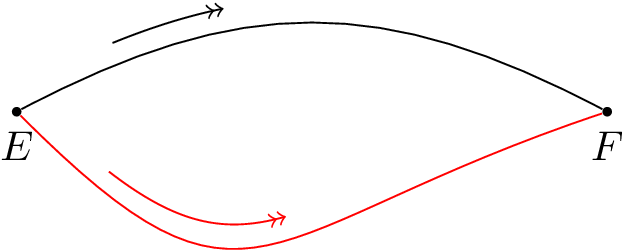

Задача построения МВО считается одной из самых простых задач вычислительной геометрии, для нее существует много различных алгоритмов. Ниже мы рассмотрим два таких алгоритма — Грэхема (Graham scan) и Джарвиса (Jarvis march). Их описание иллюстрируется кодом на Питоне. Обоим алгоритмам потребуется функция rotate, побробно описанная в предыдущем моем посте. Напомню, что эта функция определяет, с какой стороны от вектора AB находится точка C (положительное возвращаемое значение соответствует левой стороне, отрицательное — правой).

def rotate(A,B,C):
  return (B[0]-A[0])*(C[1]-B[1])-(B[1]-A[1])*(C[0]-B[0])


Этот алгоритм является трехшаговым. На первом шаге ищется любая точка в A, гарантированно входящая в МВО. Нетрудно сообразить, что такой точкой будет, например, точка с наименьшей x-координатой (самая левая точка в A). Эту точку (будем называть ее стартовой) перемещаем в начало списка, вся дальнейшая работа будет производиться с оставшимися точками. По некоторым соображениям, исходный массив точек A нами меняться не будет, для всех манипуляций с точками будем использовать косвенную адресацию: заведем список P, в котором будут хранится номера точек (их позиции в массиве A). Итак, первый шаг алгоритма заключается в том, чтобы первой точкой в P оказалась точка с наименьшей x-координатой. Код:

def grahamscan(A):
  n = len(A) # число точек
  P = range(n) # список номеров точек
  for i in range(1,n):
    if A[P[i]][0]<A[P[0]][0]: # если P[i]-ая точка лежит левее P[0]-ой точки
      P[i], P[0] = P[0], P[i] # меняем местами номера этих точек


Второй шаг в алгоритме Грэхема — сортировка всех точек (кроме P[0]-ой), по степени их левизны относительно стартовой точки R=AP[0]. Будем говорить, что B<C, если точка С находится по левую сторону от вектора RB.


Для выпонения такого упорядочивания можно применять любой алгоритм сортировки, основанный на попарном сравнении элементов, например, быструю сортировку. По некоторым причинам (главная из которых — корявость* рук), я буду использовать сортировку вставками.
*я буду очень признателен тем, кто сможет мне объяснить, как применить в данном случае встроенную питоновскую сортировку…

Итак, сортировка вставками (не забываем про косвенную адресацию и про то, что нулевая точка не сортируется):

  for i in range(2,n):
    j = i
    while j>1 and (rotate(A[P[0]],A[P[j-1]],A[P[j]])<0): 
      P[j], P[j-1] = P[j-1], P[j]
      j -= 1


Результат сортировки можно проиллюстрировать следующим рисунком.


Если мы теперь соединим точки в полученном порядке, то получим многоугольник, который, однако, не является выпуклым.


Переходим к третьему действию. Все, что нам осталось сделать, так это срезать углы. Для этого нужно пройтись по всем вершинам и удалить те из них, в которых выполняется правый поворот (угол в такой вершине оказывается больше развернутого). Заводим стек S (реально список) и помещаем в него первые две вершины (они, опять же, гарантированно входят в МВО).

  S = [P[0],P[1]]


Затем просматриваем все остальные вершины, и отслеживаем направление поворота в них с точки зрения последних двух вершин в стеке S: если это направление отрицательно, то можно срезать угол удалением из стека последней вершины. Как только поворот оказывается положительным, срезание углов завершается, текущая вершина заносится в стек.

  for i in range(2,n):
    while rotate(A[S[-2]],A[S[-1]],A[P[i]])<0:
      del S[-1] # pop(S)
    S.append(P[i]) # push(S,P[i])


В итоге в стеке S (который теперь можно рассматривать, как список) оказывается искомая последовательность вершин, причем в нужной нам ориентации, определяющая МВО заданного множества точек A.

  return S


Сложность первого и последнего шагов алгоритма является линейной по n (хотя в последнем случае имеется вложенный цикл, однако, каждая вершина внутри этого цикла ровно один раз заносится в стек, и не более одного раза оттуда удаляется), следовательно, сложность всего алгоритма определяется вторым шагом — сортировкой, именно поэтому сортировка вставкой оказывается не лучшим вариантом при больших n. Если ее заменить на быструю сортировку, то получим суммарную сложность алгоритма O(nlogn). Можно ли улучшить это время? Если алгоритм основан на попарном сравнении точек (как у нас), то доказано, что данная оценка в общем случае не улучшаема. С этой точки зрения алгоритм Грэхема оптимален. Тем не менее у него имеется не очень хорошая особенность — он не является адаптивным в том смысле, что не важно, сколько вершин в итоге войдет в МВО (три, пять, десять или n), все равно время будет линейно-логарифмическим. Такой адаптивностью обладает алгоритм Джарвиса, к рассмотрению которого мы плавно и переходим.

Полный код алгоритма Грэхема

def grahamscan(A):
  n = len(A) # число точек
  P = range(n) # список номеров точек
  for i in range(1,n):
    if A[P[i]][0]<A[P[0]][0]: # если P[i]-ая точка лежит левее P[0]-ой точки
      P[i], P[0] = P[0], P[i] # меняем местами номера этих точек 
  for i in range(2,n): # сортировка вставкой
    j = i
    while j>1 and (rotate(A[P[0]],A[P[j-1]],A[P[j]])<0): 
      P[j], P[j-1] = P[j-1], P[j]
      j -= 1
  S = [P[0],P[1]] # создаем стек
  for i in range(2,n):
    while rotate(A[S[-2]],A[S[-1]],A[P[i]])<0:
      del S[-1] # pop(S)
    S. append(P[i]) # push(S,P[i])
  return S


Алгоритм Джарвиса (другое название — алгоритм заворачивания подарков) концептуально устроен проще алгоритма Грэхема. Он является двухшаговым и не требует сортировки. Первый шаг точно такой же — нам нужна стартовая точка, которая гарантированно входит в МВО, берем самую левую точку из A.

def jarvismarch(A):
  n = len(A)
  P = range(n)
  for i in range(1,n):
    if A[P[i]][0]<A[P[0]][0]: 
      P[i], P[0] = P[0], P[i]


На втором шаге алгоритма строится МВО. Идея: делаем стартовую вершину текущей, ищем самую правую точку в A относительно текущей вершины, делаем ее текущей и т.д. Процесс завершается, когда текущей вновь окажется стартовая вершина. Как только точка попала в МВО, больше ее можно не учитывать. Поэтому заведем еще один список H, в котором в правильном порядке будут храниться вершины МВО. В этот список сразу же заносим стартовую вершину, а в списке P эту вершину переносим в конец (где мы ее в конце концов найдем и завершим алгоритм).

  H = [P[0]]
  del P[0]
  P.append(H[0])


Теперь организуем бесконечный цикл, на каждой итерации которого ищем самую левую точку из P относительно последней вершины в H. Если эта вершина стартовая, то прерываем цикл, если нет — то переносим найденную вершину из P в H. После завершения цикла в H находится искомая оболочка, которую мы и возвращаем в качестве результата.

  while True:
    right = 0
    for i in range(1,len(P)):
      if rotate(A[H[-1]],A[P[right]],A[P[i]])<0:
        right = i
    if P[right]==H[0]: 
      break
    else:
      H.append(P[right])
      del P[right]
  return H


Хм, мне удалось рассказать об алгоритме Джарвиса, не используя картинок. Следующий рисунок иллюстрирует все!


Оценим сложность алгоритма Джарвиса. Первый шаг линеен по n. Со вторым все интереснее. У нас имеется вложенный цикл, число внешних итераций равно числу вершин h в МВО, число внутренних итераций не превышает n. Следовательно, сложность всего алгоритма равна O(hn). Необычным в этой формуле является то, что сложность определяется не только длиной входных данных, но и длиной выхода (output-sensitive algorithm). А дальше как

карты

точки лягут. В худшем случае все точки из A входят в МВО (т.е. A уже само по себе выпуклый многоугольник), тогда h=n и сложность подскакивает до квадратичной. В лучшем случае (при условии, что точки из A не лежат на одной прямой) h=3 и сложность становится линейной. Осталось заранее понять, какой у нас случай, что сделать не так просто (если у вас нет машины времени**), можно только исходить из характера задачи — если точек много и они равномерно заполняют некоторую область, то (возможно) Джарвис будет быстрее, если же данные собраны на границе области, то быстрее будет Грэхем, как-то так…

**Машина времени вообще полезная штука с точки зрения алгоритмов, любая задача, требующая триллиона лет вычислений, с ее помощью может быть решена практически мгновенно — запускаем программу, садимся в машину времени, «летим» в будущее, считываем результат, возвращаемся назад. Осталось придумать, как обеспечить бесперебойную работу компьютера на пару триллионов лет…

Полный код алгоритма Джарвиса

def jarvismarch(A):
  n = len(A)
  P = range(n)
  # start point
  for i in range(1,n):
    if A[P[i]][0]<A[P[0]][0]: 
      P[i], P[0] = P[0], P[i]  
  H = [P[0]]
  del P[0]
  P.append(H[0])
  while True:
    right = 0
    for i in range(1,len(P)):
      if rotate(A[H[-1]],A[P[right]],A[P[i]])<0:
        right = i
    if P[right]==H[0]: 
      break
    else:
      H.append(P[right])
      del P[right]
  return H


На мой взгляд, задача построения минимальных выпуклых оболочек — хороший способ войти в тему вычислительной геометрии, достаточно легко придумать свой собственный алгоритм (однако, наверняка это будет вариация алгоритма Джарвиса). Утверждается, что приложений у этой задачи много, большая их часть связана с распознаванием образов, кластеризацией и т. п. Кроме того, задача построения МВО используется в качестве вспомогательного средства при решении более сложных задач вычислительной геометрии. Да, стоит отметить, что у этой задачи имеется весьма интересное трехмерное обобщение.

Спасибо всем за внимание!

Концепция поверхности на основе TIN—ArcMap

Доступно с лицензией 3D Analyst.

  • Узлы
  • Ребра
  • Треугольники
  • Оболочка
  • Топология (Topology)
  • Как хранится TIN

Модель данных поверхности TIN состоит из узлов, ребер, треугольников, полигонов оболочки и топологии.

Узлы

Узлы являются основными функциональными блоками TIN. Источниками узлов являются точки и вершины линий, содержащиеся во входных источниках данных. Каждый узел участвует в триангуляции TIN. Каждый узел модели поверхности TIN должен иметь z-значение.

Ребра

Каждый узел соединяется с ближайшими к нему узлами посредством ребер, в результате формируются треугольники, которые удовлетворяют критерию Делоне. Каждое ребро имеет два узла, а узел может иметь два ребра и более. Поскольку ребра на каждом конце имеют по узлу с z-значением, можно вычислить склон вдоль ребра между узлами.

Каждый пространственный объект из источников входных данных, использующийся для построения TIN, обрабатывается в соответствии с типом поверхности. Линии перегиба в TIN триангуляции всегда обрабатываются как ребра. Эти ребра маркируются внутри TIN как hard или soft.

Треугольники

Каждая треугольная грань описывает поведение участка поверхности TIN. Значения координат x, y и z трех узлов треугольника могут использоваться для описания грани, например, уклона, экспозиции, площади и длины поверхности. Рассматривая весь набор треугольников в целом, можно получить дополнительную информацию о поверхности, включая объем, профили поверхности и видимость.

Поскольку каждая грань демонстрирует определенное поведение поверхности, важно убедиться, что опорные точки выбраны максимально точно, для вычисления наиболее качественной поверхности. Модель TIN поверхности может оказаться неудачной, если опорные точки в важных областях расставлены неверно.

Оболочка

Оболочка TIN формируется одним или несколькими полигонами, содержащими полный набор точек, использующихся для построения TIN. Полигоны оболочки определяют зону интерполяции TIN. Внутри или на ребре полигонов оболочки можно интерполировать z-значения поверхности, выполнять анализ и генерировать отображение поверхности. Вне полигонов оболочки, информацию о поверхности получить нельзя. Оболочка TIN может состоять из одного или нескольких полигонов, которые могут быть невыпуклыми.

Невыпуклая оболочка должна задаваться пользователем при построении TIN с помощью включения исключающих пространственных объектов (вырезающих и стирающих). Эти объекты явно определяют ребро поверхности. Если для задания оболочки не использовались исключающие объекты, генератор TIN создаст выпуклую оболочку для задания краевых ребер TIN. Выпуклая оболочка – это полигон, любая линия которого, соединяющая любые две точки TIN, должна проходить внутри или задавать ребро выпуклой оболочки. Задание невыпуклой оболочки позволяет избежать генерации ошибочной информации в областях TIN, которые лежат за пределами текущего набора данных, но в пределах выпуклой оболочки. Рассмотрите диаграмму, приведенную ниже.

Без использования вырезающих объектов, в закрашенных областях могут быть интерполированы неверные значения.

Топология (Topology)

Топологическая структура TIN определяется информацией, которая формируется на основе базовых данных о каждом узле треугольника, количестве ребер, типе и соседстве с остальными треугольниками. Для каждого треугольника, TIN хранит:

  • Номер треугольника
  • Номера каждого соседнего треугольника
  • Три узла, задающие этот треугольник
  • Координаты x,y каждого узла
  • Z-значение поверхности каждого узла
  • Тип каждого ребра треугольника (hard или soft)

Кроме того, TIN поддерживает список всех ребер, которые формируют оболочку TIN и информацию, определяющую проекцию TIN и единицы измерения.

Как хранится TIN

Как и покрытие, TIN хранится в виде файлов в отдельной папке. Однако, TIN не является покрытием, поэтому не имеет ассоциированных файлов INFO. Папка TIN содержит семь файлов, в которых хранится информацию о поверхности TIN. Эти файлы имеют бинарный формат и не читаются обычными текстовыми редакторами.

Вогнутые и выпуклые: основные различия, которые необходимо знать 3

РАЗРЕШЕНИЕ

Принадлежит YourDictionary, Copyright YourDictionary 

Важно знать разницу между вогнутым и выпуклым, потому что эти два слова имеют противоположные значения. Смешение этих терминов в письме может привести к значительным недоразумениям. Освойте основные различия, чтобы вы могли использовать слова вогнутый и выпуклый в вашем словаре с уверенностью.

Вогнутый против выпуклого

Слова вогнутый и выпуклый встречаются на многих уроках математики и естественных наук. Эти два слова тесно связаны друг с другом. Оба слова могут использоваться как существительное или прилагательное. Они отличаются тем, что каждое слово описывает определенную форму. Вогнутая форма противоположна выпуклой форме.

Использование прилагательного

Термины вогнутый и выпуклый чаще всего используются в качестве прилагательных. При использовании в качестве прилагательного эти слова описывают форму объекта, указывая, изогнут ли объект внутрь или наружу.

  • Предмет с вогнутой формой изгибается внутрь, например, ложка или миска. Середина тоньше, чем края.
  • Объект с выпуклой формой — это объект, выгнутый наружу, например баскетбольный или бейсбольный мяч. Середина толще, чем края.

Слова вогнутый и выпуклый описывают направление, в котором изгибается объект. Поскольку вогнутые формы изгибаются внутрь, а выпуклые изгибаются наружу, каждое из этих двух слов описывает противоположные формы.

Реклама

Использование существительного

Слова вогнутый или выпуклый могут использоваться как существительные. При таком использовании термины будут использоваться для обозначения конкретных вещей, а не для описания формы другого объекта.

  • Вогнутость — это любая линия или поверхность, изгибающаяся внутрь. (Эта линия вогнутая.)
  • Выпуклая — это любая линия или поверхность, изгибающаяся наружу. (Эта поверхность выпуклая.)

Использование вогнутых или выпуклых поверхностей таким способом не так распространено. Гораздо чаще эти термины используются в качестве прилагательных.

Как запомнить разницу между вогнутой и выпуклой

Запомнить, в какой форме (выпуклой или вогнутой) кривые может быть сложно, потому что эти два термина звучат очень похоже. Чтобы убедиться, что вы помните, какое слово представляет какую фигуру, используйте этот простой прием.

  • Если что-то прогибается-в , значит проваливается внутрь. Вогнутая содержит слово пещера .
  • Помните, впадина идет внутрь, поэтому вогнутая форма должна кривая в .
  • Выпуклая содержит ex . Ex это начало слова выход . Когда вы выходите, что вы делаете? Вы выходите.
  • Свяжите ex в выпуклость с выходом. Это может помочь вам вспомнить, что выпуклая форма изгибается .

Реклама

Вогнутые и выпуклые в реальном мире

В реальном мире существует несколько примеров вогнутых и вогнутых форм. От походов в парк развлечений до очков для коррекции зрения — концепции вогнутости и выпуклости влияют на многие аспекты повседневной жизни. Это одна из причин, почему так важно правильно использовать эти термины.

Вогнутые и выпуклые зеркала

Если вы когда-нибудь стояли перед зеркалом, которое заставляло вас казаться другого размера, чем вы есть на самом деле, вы видели в действии либо выпуклое, либо вогнутое зеркало, а может быть, и то, и другое. В домах развлечений в парках развлечений часто есть оба вида зеркал, чтобы поразить посетителей тем, насколько по-разному их изображение может выглядеть от одного зеркала к другому.

  • Зеркала, которые делают вас меньше, чем вы есть на самом деле, — это выпуклые зеркала. Зеркало этого типа изогнуто наружу.
  • Зеркала, которые заставляют вас казаться больше, чем вы есть на самом деле, вогнуты. Посмотрите внимательно, и вы увидите, что этот тип зеркала изгибается внутрь.

Реклама

Вогнутость и выпуклость в кривых позвоночника

Вместо того, чтобы быть прямым вверх и вниз, позвоночник (позвоночник) человека имеет изгибы. Не у всех позвоночник имеет одинаковые изгибы, так как есть несколько факторов, которые могут точно повлиять на то, где и как изгибается позвоночник человека. Однако позвоночник имеет как вогнутые, так и выпуклые изгибы.

  • ОПИСАНИЕ

    вогнуто-выпуклые искривления позвоночника

  • ИСТОЧНИК

    Пиковит44 Используется по лицензии Getty Images

  • Когда позвоночник человека изгибается внутрь, к передней части тела человека, это вогнутая кривая.
  • Когда позвоночник человека изгибается наружу, в сторону от его или ее передней стороны, это выпуклая кривая.

Вогнутые и выпуклые линзы в очках

Линзы в очках — это не просто плоские кусочки стекла. Тип проблемы со зрением у человека будет влиять на то, будут ли его очки иметь вогнутые или выпуклые линзы. В некоторых очках, таких как бифокальные, используются оба типа очков.

  • Вогнутые линзы разделяют лучи света. Этот тип линз используется для коррекции близорукости (близорукости).
  • Выпуклые линзы фокусируют световые лучи, что позволяет формировать изображение. Они используются для коррекции дальнозоркости (гиперметропии).

Объявление

Разбираемся в научной терминологии

Чем глубже вы будете изучать математику и естественные науки, тем больше научной терминологии вам потребуется освоить. Теперь, когда вы знаете разницу между вогнутым и выпуклым, самое время изучить другой научный жаргон. Начните с изучения базовой таксономии живых существ. Затем откройте для себя тонкие различия между другими научными терминами, такими как масса и вес. Оттуда вы можете изучить некоторые примеры органических соединений. Всегда есть новые термины для изучения и концепции для изучения!

Вогнутая вверх и вниз

     
Вогнутость вверх при увеличении наклона:  
Вогнутая вниз при уменьшении наклона:  

Что если наклон останется прежним (прямая линия)? Это может быть и то, и другое! См. сноску.

Вот еще несколько примеров:

Вогнутая вверх также называется Выпуклая или иногда Выпуклая вниз

Вогнутая вниз также называется Вогнутая или иногда Выпуклая вверх

Вогнутая вниз

Поиск где…

Обычно наша задача состоит в том, чтобы найти , где кривая вогнута вверх или вогнута вниз:

Определение

Линия, проведенная между любыми двумя точками на кривой, не будет пересекать кривую:

Давайте составим для этого формулу!

Во-первых, строка: возьмите любые два разных значения a и b (в интервале, который мы смотрим):

Затем «скользите» между a и b , используя значение t (от 0 до 1):

х = ta + (1−t)b

  • Когда t=0 получаем x = 0a+1b = b
  • Когда t=1 , мы получаем x = 1a+0b = a
  • Когда t находится в диапазоне от 0 до 1, мы получаем значения между a и b

Теперь определите высоты для этого значения x:

 

Когда x = ta + (1−t)b :

  • Кривая y = f( ta + (1−t)b )
  • Линия на y = tf(a) + (1−t)f(b)

И (для вогнутая вверх ) линия не должна быть ниже кривой:

Для вогнутая вниз линия не должна быть выше кривой ( ≤ становится ≥ ):

И это фактические определения вогнутых вверх и вогнутых вниз .

Вспоминая

Какой путь какой? Подумайте:

C oncave Up вардов = CUP

Исчисление

Производные могут помочь! Производная функции дает наклон.

  • Когда наклон постоянно увеличивается , функция вогнута вверх .
  • Когда наклон постоянно уменьшается , функция вогнута вниз .

Взятие второй производной на самом деле говорит нам, постоянно ли наклон увеличивается или уменьшается.

  • Когда вторая производная положительна , функция вогнута вверх .
  • Когда вторая производная отрицательна , функция вогнута вниз .

Пример: функция x

2

Ее производная равна 2x (см. Правила производных)

2x постоянно увеличивается, поэтому функция вогнута вверх .

Его вторая производная равна 2

2 равно положительному , поэтому функция вогнута вверх .

Оба дают правильный ответ.

 

Пример: f(x) = 5x

3 + 2x 2 − 3x

Вычислим вторую производную:

  • . 3 (с использованием Power Rule)
  • Вторая производная равна f»(x) = 30x + 4 (используя степенное правило)

 

И 30x + 4 отрицательно до x = -4/30 = -2/15, а далее положительно. Итак:

f(x) равно вогнутой вниз вверх до x = −2/15

f(x) равно вогнутой вверх от x = −2/15 на

 

Примечание. изменений называется точкой перегиба.

 

Сноска: уклон остается прежним

Что делать, если уклон остается прежним (прямая линия)?

Прямая линия допустима для вогнутой вверх или вогнутой вниз .

Но когда мы используем специальные термины строго вогнутая вверх или строго вогнутая вниз , тогда прямая линия — это , а не .

Пример: y = 2x + 1

2x + 1 — прямая.