Содержание
Постигая кривые Безье | CAT.IN.WEB
Кривые Безье — это способ определения кривой по опорным точкам.
Для наглядности можно рассматривать их как график передвижения точки от начала до конца маршрута в зависимости от времени движения.
Время изменяется от 0 до 1 (до 100%). То есть мы изначально знаем время, за которое нужно переместиться из начальной точки (P0) в конечную (Pn) (конкретная величина не имеет значения). На основании этого времени можно вычислить точную траекторию — по формулам.
Берем все время за 100% (или за единицу). В момент 0 (0%) точка находится в точке P0, в момент 1 (100%) – в точке Pn. Положение точки в любой момент между этими моментами можно вычислить по формуле.
Порядок кривой всегда на 1 меньше количества контрольных точек. Рассмотрим построение пошагово, начиная с самой простой кривой.
Кривая Безье первого порядка
Простейшая кривая Безье — это обычная линия. Порядок первый – значит, контрольных точек две. Ее академическое уравнение выглядит так:
Порядок первый – значит, контрольных точек две. Ее академическое уравнение выглядит так:
B(t) = (1-t)*P0 + t*P1
А график — вот так:
Разберем на простейшем примере. Пусть:
- первая контрольная точка — P0 имеет координаты (0; 0),
- вторая (и последняя) – P1 – (5; 0).
Сразу же проверим формулу.
При t = 0 (в начальный момент времени) должна получиться точка P0, а при t = 1 должна получиться точка P1.
- B(0) = (1-0)*P0 + 0*P1 = P0 — (0; 0)
- B(1) = (1-1)*P0 + 1*P1 = P1 — (5; 0)
А теперь найдем несколько точек между началом и концом. Тут используется сложение и умножение векторов, но в данном случае все интуитивно понятно:
B(0.1) = (1-0.1)*P0 + 0.1*P1 = 0.9*P0 + 0.1*P1 = 0.9*(0;0) + 0. 1*(5;0) = (0.5; 0)
1*(5;0) = (0.5; 0)B(0.2) = (1-0.2)*P0 + 0.2*P1 = 0.8*P0 + 0.2*P1 = 0.8*(0;0) + 0.2*(5;0) = (1; 0)B(0.3) = (1-0.3)*P0 + 0.3*P1 = 0.7*P0 + 0.3*P1 = 0.7*(0;0) + 0.3*(5;0) = (1.5; 0)B(0.4) = (1-0.4)*P0 + 0.4*P1 = 0.6*P0 + 0.4*P1 = 0.6*(0;0) + 0.4*(5;0) = (2; 0)B(0.5) = (1-0.5)*P0 + 0.5*P1 = 0.5*P0 + 0.5*P1 = 0.5*(0;0) + 0.5*(5;0) = (2.5; 0)B(0.6) = (1-0.6)*P0 + 0.6*P1 = 0.4*P0 + 0.6*P1 = 0.4*(0;0) + 0.6*(5;0) = (3; 0)B(0.7) = (1-0.7)*P0 + 0.7*P1 = 0.3*P0 + 0.7*P1 = 0.3*(0;0) + 0.7*(5;0) = (3.5; 0)B(0.8) = (1-0.8)*P0 + 0.8*P1 = 0.2*P0 + 0.8*P1 = 0. 2*(0;0) + 0.8*(5;0) = (4; 0)
2*(0;0) + 0.8*(5;0) = (4; 0)B(0.9) = (1-0.9)*P0 + 0.9*P1 = 0.1*P0 + 0.9*P1 = 0.1*(0;0) + 0.9*(5;0) = (4.5; 0)
Все полученные точки лежат на одной прямой – это и есть кривая Безье первого порядка.
Время идет, точка движется от старта к финишу. И в любой момент времени мы точно знаем, где она находится.
Кривые Безье второго порядка и больше
В определении кривых Безье выше первого порядка кроме начала и конца появляются дополнительные опорные точки, смысл которых сложно понять с первого захода.
Непосредственно через них кривая не проходит, так зачем же они нужны?
На самом деле эти точки определяют направление движения (направление изгиба кривой) и крутизну этого изгиба.
Квадратичная кривая
Кривая Безье второго порядка, или квадратичная, задается тремя контрольными точками:
- P0 – начало;
- P2 – конец;
- P1 – вспомогательная точка, определяющая изгиб кривой.

Маленький спойлер: кривая Безье второго порядка имеет форму параболы (не обязательно симметричной).
Формула у нее вот такая:
B(t) = (1 - t)2*P0 + 2t*(1 - t)*P1 + t2*P2
Проверим, что в начале и конце движения мы окажемся в точках P0 и P2 соответственно:
- B(0) = (1 — 0)2 *P0 + 2*0*(1 — 0) * P1 + 02*P2 = P0
- B(1) = (1 — 1)2 *P0 + 2*1*(1 — 1) * P1 + 12*P2 = P2
На примере:
- P0 (-1; 0)
- P2 (1; 0)
- опорная точка P1 (0; 2):
Найдем, где будет точка через половину времени t (0.5):
B(0.5) = 0.25*P0 + 0.5*P1 + 0.25*P2 = (-0.25; 0) + (0; 1) + (0.25; 0) = (0; 1)
То есть на половине временного интервала мы окажемся в точке (0; 1).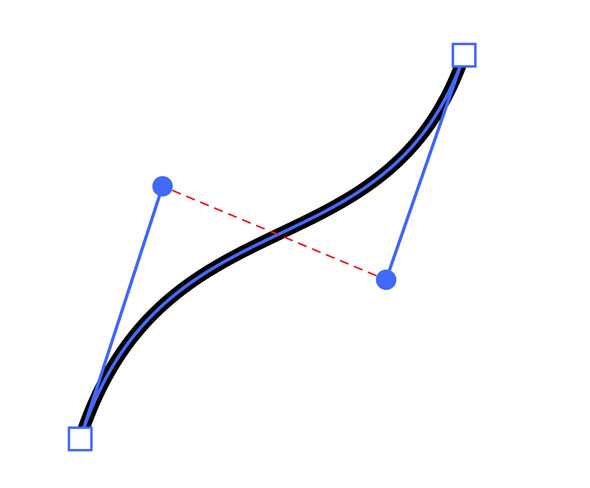
Если найти еще несколько точек, вырисуется ровная парабола. Так, в общем, и было задумано для простоты вычислений и визуальной ясности.
Рекурсивность кривых Безье
Волшебство кривых Безье заключается в том, что они рекурсивны. То есть умея строить кривую первого порядка, мы можем построить и квадратичную кривую, даже не зная ее формулы.
Вернемся к предыдущему примеру:
- P0 (-1; 0)
- P2 (1; 0)
- опорная точка P1 (0; 2):
Предположим, что мы не знаем, как построить кривую второго порядка между P0 и P2. Но мы можем построить простейшую кривую первого порядка между P0 и P1, а также между P1 и P2, пользуясь формулой:
B(t) = (1-t)*P0 + t*P1
Для каждого момента времени мы можем найти положение точки на каждой из этих кривых.
Например, в момент времени 0.25 соответствующие точки Q0 и Q1 будут в таких позициях:
Между этими точками тоже можно построить кривую первого порядка.
Магия заключается в том, что точка на этой кривой в момент времени t = 0.25 соответствует точке на искомой кривой второго порядка в этот же момент времени.
Распишем чуть подробнее.
Мы хотим найти точку на кривой второго порядка P0-P11-P2 в момент времени t.
- Этому моменту на кривой P0-P1 соответствует точка Q0;
- А на кривой P1-P2 – точка Q1.
Искомая точка – это точка на кривой Q0-Q1, соответствующая моменту времени t.
Этот рекурсивный алгоритм построения кривой Безье носит имя Поля де Кастельжо.
Кубическая кривая
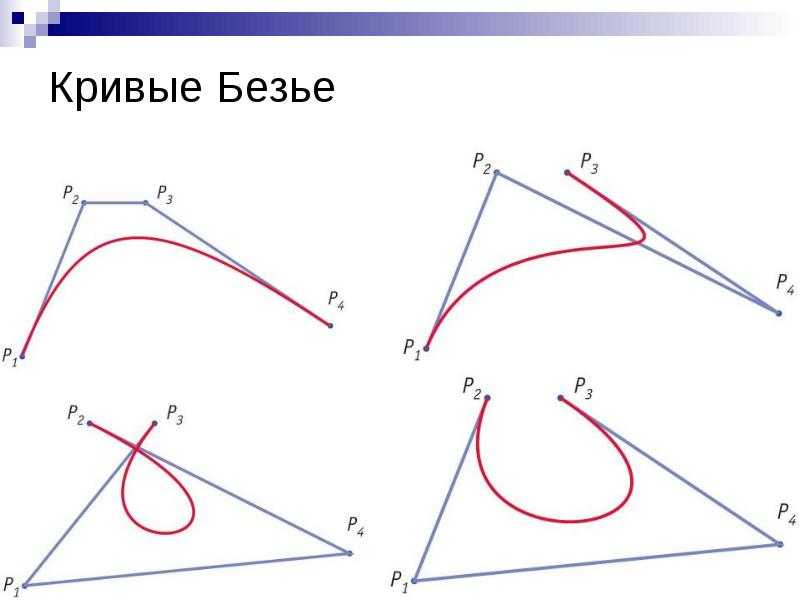
Кривая Безье третьего порядка, или кубическая кривая, определяется уже четырьмя опорными точками – началом, концом и двумя вспомогательными, через которые она не будет непосредственно проходить.
Две вспомогательные точки снова определяют направление и крутизну изгибов кривой.
Формула кубической кривой еще сложнее:
B(t) = (1 - t)3*P0 + 3t*(1-t)2*P1 + 3t2*(1 - t)*P2 + t3*P3
Вы можете попробовать эту кривую рассчитать самостоятельно.
Обратите внимание, ее тоже можно получить рекурсивно!
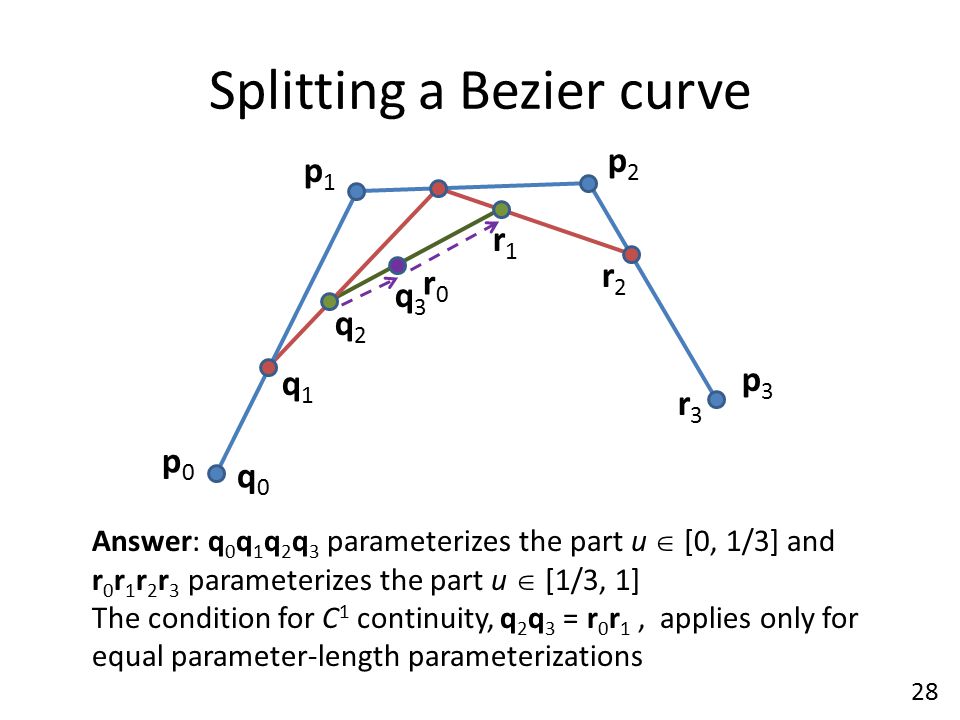
Найти точку кривой третьего порядка в момент времени t можно по следующему алгоритму:
- Строим кривые первого порядка P0-P1, P1-P2, P2-P3
- Находим на них соответствующие t точки Q0, Q1, Q2
- Строим кривые первого порядка Q0-Q1 и Q1-Q2
- Находим на них соответствующие t точки R0 и R1
- Строим кривую первого порядка R0-R1
- Находим на ней точку, соответствующую
t.
Зачем все это нужно?
Круто, теперь мы умеем строить кривые Безье любого порядка, но зачем нам это нужно? Каково практическое применение этих построений?
Кривые Безье используются в описаниях шрифтов TrueType, в SVG, GIMP и других графических форматах, в 3D-графике. Они используются даже в CSS для описания плавности анимации.
Они используются даже в CSS для описания плавности анимации.
В общем, штука очень полезная.
Описание и примеры стандартных функций SVG
Доминирующей причиной появления этого блога стало незаслуженное забвение на целых десять лет языка разметки масштабируемой векторной графики – SVG (Scalable Vector Graphics), входящего в подмножество расширяемого языка разметки XML.
Стандарт SVG 1.0 был принят в качестве спецификации Консорциумом Всемирной паутины (W3C) в сентябре 2001 г. Стандарт SVG 1.1 и его версии SVG mobile profiles (SVG Basic and SVG Tiny) были приняты консорциумом в качестве рекомендации в январе 2003 г.
Сейчас ведутся работы по созданию стандарта SVG 2.0
Основные преимущества формата SVG.
Я не буду долго распространяться о преимуществах векторной графики перед растровой в вебдизайне, замечу лишь, что, однажды созданный, файл в формате SVG одинаково хорошо выглядит без потери качества и на мобильном устройстве и на станционарном мониторе домашнего ПК.
Шапка данного сайта выполнена в формате SVG, попробуйте уменьшить окно браузера до минимальных размеров, картинка на “лету” будет также пропорционально уменьшаться.
SVG – это двухмерная графика и тем не менее это текстовый формат, который можно легко править в блокноте или просто рисовать в векторных редакторах: Incscape , Adobe illustrator, CorelDRAW
Бесконечное полотно документа svg.
Итак, как происходит формирование векторного изображения.
Документ формата SVG – это двухмерный объект, который может иметь бесконечные координаты, как в положительном, так и в отрицательном направлении по осям X и Y. Также документ SVG имеет две области просмотра: viewport – системная область просмотра и viewBox – пользовательская область просмотра, положение которой относительно начала системных координат viewport, может задаваться собственной, пользовательской системой координат. Другими словами окно просмотра viewBox, может быть перемещёно в любое место документа SVG, при этом берется фрагмент изображения под ним, который после процесса согласования между viewBox и viewport, возвращается обратно в системную область просмотра viewport, которую видит пользователь. Используя это свойство можно организовать вертикальную или горизонтальную прокрутку изображения, меняя параметры координат viewBox.
Используя это свойство можно организовать вертикальную или горизонтальную прокрутку изображения, меняя параметры координат viewBox.
При уменьшении размера пользовательского окна просмотра viewbox можно пропорционально увеличивать фрагмент изображения в системной области просмотра или уменьшать его при увеличении размера viewbox.
Таким образом реализуется эффект лупы. Более подробно эти процессы разобраны в статье: Трансформация изображений SVG при изменении параметров Viewbox.
Взаимодействие SVG, XML с HTML, CSS, Jscript
В SVG, как и в HTML можно добавлять ссылки на внешние ресурсы. Но если в HTML одна картинка может служить только для одной внешней ссылки, то в SVG документ можно добавлять сколько угодно внешних ссылок . Картинка кликабельна.
Внутрь HTML страницы легко встраивается код SVG документа или целиком подключается внешний SVG файл. Можно наоборот, внутри SVG файла разместить код HTML внутри тегов foreignObject. Получаются интересные эффекты: Внутри SVG файла находится работающий внешний HTML сайт. К SVG формату можно подключать внешние таблицы стилей CSS 2.0, что позволяет управлять сразу несколькими файлами *.svg. Также вполне допустимо подключение стилей внутри файла *.svg внутри тегов style или использовать внутренние стили непосредственно внутри командных строк фигур и путей.
К SVG формату можно подключать внешние таблицы стилей CSS 2.0, что позволяет управлять сразу несколькими файлами *.svg. Также вполне допустимо подключение стилей внутри файла *.svg внутри тегов style или использовать внутренние стили непосредственно внутри командных строк фигур и путей.
SVG, как любой основанный на XML формат, позволяет использовать для его обработки таблицы трансформации (XSLT).
Преобразуя XML-данные в SVG с помощью простого XSL, можно получить графическое представление текстовых данных, например визуализировать графики, круговые диаграммы, гистограммы и т.д.
Анимация и интерактивность SVG.
Анимация в SVG осуществляется при помощи языка SMIL (Synchronized Multimedia Integration Language). Также поддерживаются скриптовые языки на основе спецификации ECMAScript — это встраиваемый расширяемый язык программирования.
То есть всё находится в одном месте, внутри документа SVG, поэтому нет необходимости для подключения внешних библиотек.
На каждую отдельную фигуру или на целое изображение можно установить обработчик событий (клик, наведение мышки, нажатие клавиши и т. д), таким образом, пользователь может управлять рисунком. Наведите курсор мышки на кнопку“Start” на примере слева.
д), таким образом, пользователь может управлять рисунком. Наведите курсор мышки на кнопку“Start” на примере слева.
По событию mouseover на этой кнопке начнется анимация по команде begin=”startButton.mouseover” – движение цветных шариков по криволинейному пути. Закончится анимация либо через заданные в коде 16 секунд, либо в любой момент по наведению курсора мышки на цветные радиокнопки “Stop”. При этом каждая радиокнопка управляет своим объектом совпадающим по цвету. На рисунке ниже анимация начинается и заканчивается при нажатии клавиши мышки на кнопки GO и STOP. В этом случае работает событие click. Команда на запуск анимации – begin=”gO.click” и соответственно остановка – end=”stop.click”
Следующий пример анимации – плавная отрисовка картинки с нуля до полного изображения.
Уже встроенные в SVG языки программирования позволяют реализовать довольно сложные сценарии анимации. Но, в дополнение к этому есть еще более мощные средства для реализации интерактивности графики и ее анимации – это внешние библиотеки сторонних разработчиков: D3. js, BonsaiJS, Svg.js, Snapsvg.js
js, BonsaiJS, Svg.js, Snapsvg.js
Еще примеры анимации ⇛
Недостатки SVG формата
- С увеличением количества мелких деталей в изображении, быстрее растёт размер файла SVG-данных. Предельный случай — когда изображение представляет собой белый шум. В этом случае SVG не только не даёт никаких преимуществ в размере файла, но даже имеет проигрыш по отношению к растровому формату. На практике, SVG становится невыгоден уже задолго до того, как изображение дойдёт до стадии белого шума.
- Трудность использования в крупных картографических приложениях из-за того, что для правильного отображения маленькой части изображения документ необходимо прочитать целиком.
- В настоящее время SVG формат применяется в Интернете сравнительно мало, из-за недостаточной кроссбраузерности. Лучше всего обстоят дела у Mozilla Firefox со встроенным просмотрщиком SVG, так как ее разработчики находятся в рабочей группе Консорциума Всемирной паутины (W3C) по разработке и внедрению стандарта SVG.
 Хуже всего дела по поддержке формата SVG у Microsoft, которая покинула группу 2003 г. Для Internet Explorer – необходим Adobe SVG Viewer (ASV). С 9 версии IE частично поддерживает функции SVG.
Хуже всего дела по поддержке формата SVG у Microsoft, которая покинула группу 2003 г. Для Internet Explorer – необходим Adobe SVG Viewer (ASV). С 9 версии IE частично поддерживает функции SVG.
Браузеры Apple Safari, Google Chrome намного лучше поддерживают SVG, но не полностью, так как SVG – это большая спецификация (вдвое больше HTML 4.01), именно поэтому разработчики браузеров внедряют функции постепенно, от версии к версии. Но абсолютно все разработчики современных браузеров заявляют, что за форматом SVG будущее в области графики вебдизайна.
UPD. Добавлен новый раздел онлайн генераторы SVG кода path.
следующая: Структура SVG документа ⇛
Графика
— Ближайшая точка на кубической кривой Безье?
Поскольку другие методы на этой странице кажутся приблизительными, этот ответ даст простое численное решение. Это реализация Python, зависящая от библиотеки numpy для предоставления класса Bezier . В моих тестах этот подход работал примерно в три раза лучше, чем моя реализация грубой силы (с использованием выборок и подразделения).
В моих тестах этот подход работал примерно в три раза лучше, чем моя реализация грубой силы (с использованием выборок и подразделения).
Посмотрите интерактивный пример здесь.
Нажмите, чтобы увеличить. 93*px_0 + …
Преобразуйте его в стандартный вид с четырьмя коэффициентами.
Вы можете записать четыре коэффициента, расширив исходное уравнение.
Расстояние от точки p до кривой B(t) можно рассчитать по теореме Пифагора.
Здесь a и b два измерения наших точек х и х . Это означает, что квадрат расстояния D(t) равен:
Сейчас я не вычисляю квадратный корень, потому что достаточно сравнить относительные квадраты расстояний. Все последующие уравнения относятся к расстоянию в квадрате .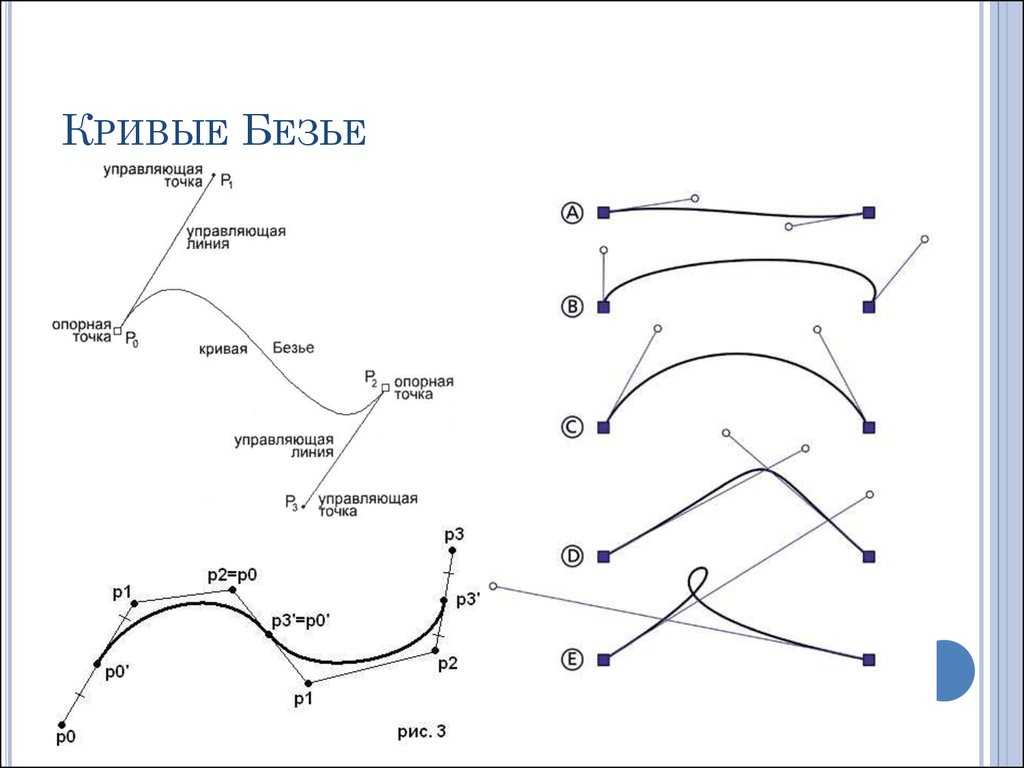
Эта функция D(t) описывает расстояние между графиком и точками. Нас интересуют минимумы в диапазоне t в [0, 1] . Чтобы их найти, мы должны вывести функцию дважды. Первая производная функции расстояния представляет собой полином 5-го порядка:
Вторая производная:
График десмоса позволяет нам исследовать различные функции.
D(t) имеет свои локальные минимумы, где d'(t) = 0 и d»(t) >= 0 . Это означает, что мы должны найти t для d'(t) = 0′ .
черный : кривая Безье, зеленый : d(t), фиолетовый : d'(t), красный :d»(t)
9 найти корни д'(т) . Я использую библиотеку numpy, которая принимает коэффициенты полинома.
dcoeffs = np.stack([da, db, dc, dd, de, df]) корни = np.roots (dcoeffs)
Удалите мнимые корни (оставьте только действительные корни) и удалите все корни, которые < 0 или > 1 . С кубическим Безье, вероятно, останется около 0-3 корней.
Затем проверьте расстояния каждого |B(t) - pt| за каждые т в корнях . Также проверьте расстояния для B(0) и B(1) , так как начало и конец кривой Безье могут быть ближайшими точками (хотя они не являются локальными минимумами функции расстояния).
Вернуть ближайшую точку.
Прикрепляю класс для Безье в питоне. Проверьте ссылку github для примера использования. 92 из
# pt и кривая
# ближайшая(pt) возвращает точку на кривой
# который ближе всего к pt
# maxes(pt) строит кривую, используя matplotlib
класс Безье (объект):
exp3 = np.array([[3, 3], [2, 2], [1, 1], [0, 0]], dtype=np.float32)
exp3_1 = np.array([[[3, 3], [2, 2], [1, 1], [0, 0]]], dtype=np.float32)
exp4 = np.array([[4], [3], [2], [1], [0]], dtype=np. 1 + d
1 + d
#
# Коэффициенты имеют ту же размерность, что и контроль
# точки.
def create_coefficients (я):
очки = личные очки
a = - очки [0] + 3 * очки [1] - 3 * очки [2] + очки [3]
b = 3*баллы[0] - 6*баллы[1] + 3*баллы[2]
с = -3*баллы[0] + 3*баллы[1]
д = очки [0]
self.coeffs = np.stack([a, b, c, d]).reshape(-1, 4, 2)
# Возвращаем точку на кривой по параметру t.
защита в (я, т):
если тип (t) != np.ndarray:
т = np.массив (т)
pts = self.coeffs * np.power (t, self.exp3_1)
вернуть np.sum (pts, ось = 1)
# Возвращает ближайшее РАССТОЯНИЕ (в квадрате) между точкой pt
# и кривая.
Защитное расстояние2 (я, pt):
точки, расстояния, индекс = self.measure_distance(pt)
обратные расстояния[индекс]
# Возвращаем ближайшую POINT между точкой pt
# и кривая.
Ближайший по определению (я, pt):
точки, расстояния, индекс = self.measure_distance(pt)
точки возврата[индекс]
# Измерить расстояние^2 и ближайшую точку на кривой
# точка pt и кривая. 2
2
# 2 Получите корни D'(t). Это крайности
# D(t) и содержат ближайшие точки на неотсеченном
# изгиб. Сохраняйте только минимумы, проверяя,
# D''(roots) > 0 и отбросить мнимые корни.
# 3 Вычислите расстояния от точки до минимумов как
# а также начало и конец кривой и возврат
# индекс кратчайшего расстояния.
#
# Этот график десмоса является полезной визуализацией.
# https://www.desmos.com/calculator/ktglugn1ya
def мера_расстояния (я, pt):
коэфф = self.coeffs
# Это коэффициенты производных d/dx и d/(d/dx).
da = 6*np.sum(коэфф[0][0]*коэфф[0][0])
db = 10*np.sum(коэфф[0][0]*коэфф[0][1])
dc = 4*(np.sum(коэфф[0][1]*коэфф[0][1]) + 2*np.sum(коэфф[0][0]*коэфф[0][2]))
dd = 6*(np.sum(коэфф[0][0]*(коэфф[0][3]-pt)) + np.sum(коэфф[0][1]*коэфф[0][2]) )
de = 2*(np.sum(coeffs[0][2]*coeffs[0][2])) + 4*np.sum(coeffs[0][1]*(coeffs[0][3]- пт))
df = 2*np.sum(коэфф[0][2]*(коэфф[0][3]-pt))
дда = 5*да
ддб = 4*дб
ддц = 3*ддц
ддд = 2*дд
дде = де
dcoeffs = np. stack([da, db, dc, dd, de, df])
stack([da, db, dc, dd, de, df])
ddcoeffs = np.stack([dda, ddb, ddc, ddd, dde]).reshape(-1, 1)
# Вычисление реальных экстремумов путем получения корней первого
# производная функции расстояния.
экстремум = np_real_roots (dcoeffs)
# Удаляем корни, выходящие за границы обрезанного диапазона [0, 1].
# [будущая ссылка] https://stackoverflow.com/questions/47100903/удаление-каждого-третьего-элемента-тензора-в-тензорном потоке
dd_clip = (np.sum(ddcoeffs * np.power(extrema, self.exp4)) >= 0) & (extrema > 0) & (extrema < 1)
минимумы = экстремумы[dd_clip]
# Добавьте начальную и конечную позиции как возможные позиции.
потенциалы = np.concatenate((минимумы, self.boundaries))
# Вычислить точки при возможных параметрах t и
# получить индекс ближайшего
точки = self.at (потенциалы. изменить форму (-1, 1, 1))
расстояния = np.sum (np.square (точки - pt), ось = 1)
индекс = np.argmin (расстояния)
точки возврата, расстояния, индекс
# Наведите кривую на фигуру из библиотеки matplotlib.
# maxes ... оси фигуры matplotlib
заговор по определению (я, максимумы):
импортировать matplotlib.path как mpath
импортировать matplotlib.patches как mpatches
Путь = mpath.Путь
pp1 = mppatches.PathPatch(
Путь(собственные.точки, [Путь.MOVETO, Путь.КРИВАЯ4, Путь.КРИВАЯ4, Путь.КРИВАЯ4]),
fc="none")#, transform=ax.transData)
pp1.set_alpha(1)
pp1.set_color('#00cc00')
pp1.set_fill(ложь)
pp2 = mppatches.PathPatch(
Путь(собственные.точки, [Путь.MOVETO, Путь.LINETO, Путь.LINETO, Путь.LINETO]),
fc="none")#, transform=ax.transData)
pp2.set_alpha(0.2)
pp2.set_color('#666666')
pp2.set_fill(ложь)
maxes.scatter(*zip(*self.points), s=4, c=((0, 0,8, 1, 1), (0, 1, 0,5, 0,8), (0, 1, 0,5, 0,8),
(0, 0,8, 1, 1)))
maxes.add_patch(pp2)
maxes.add_patch (pp1)
# Обертка вокруг np.roots, но возвращает только реальный
# корни и игнорирование мнимых результатов.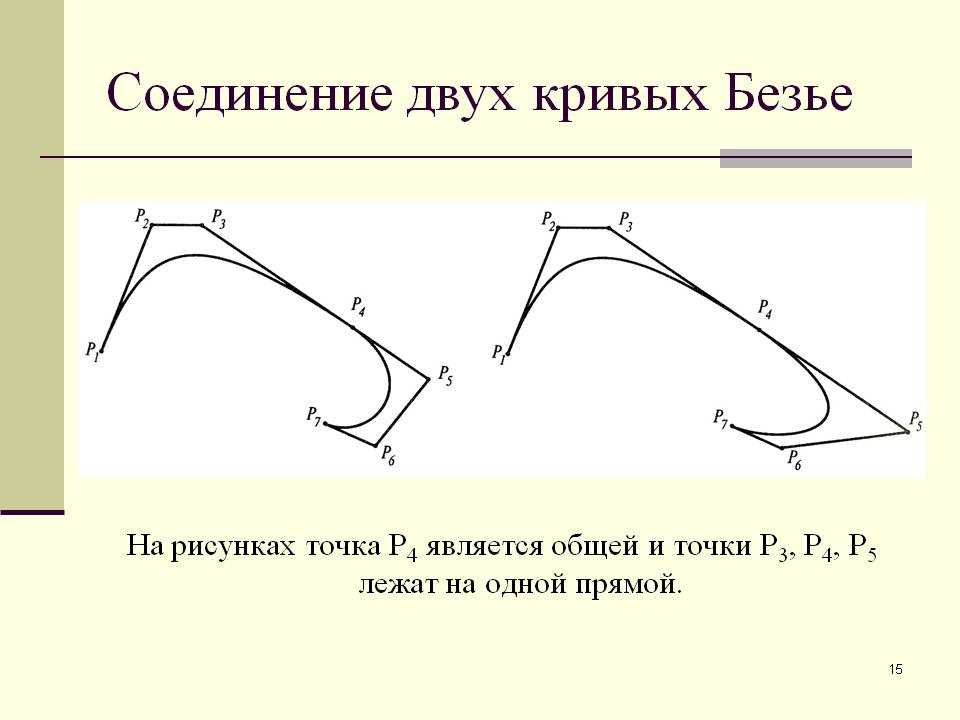
def np_real_roots (коэффициенты, EPSILON = 1e-6):
r = np.roots (коэффициенты)
вернуть r.real[abs(r.imag) < EPSILON]
математика - Как рассчитать третью контрольную точку квадратичной кривой Безье?
спросил
Изменено
2 года, 4 месяца назад
Просмотрено
794 раза
Я понимаю, как интерполировать положение кривых Безье. Но мне любопытно, как я могу рассчитать третью контрольную точку, если у меня есть только две (2) контрольные точки ( Start & End ), а также интерполированное положение квадратичной кривой Безье. Например, если у меня есть только A и C , как я могу рассчитать значение B .
Смотрите на эту картинку:
.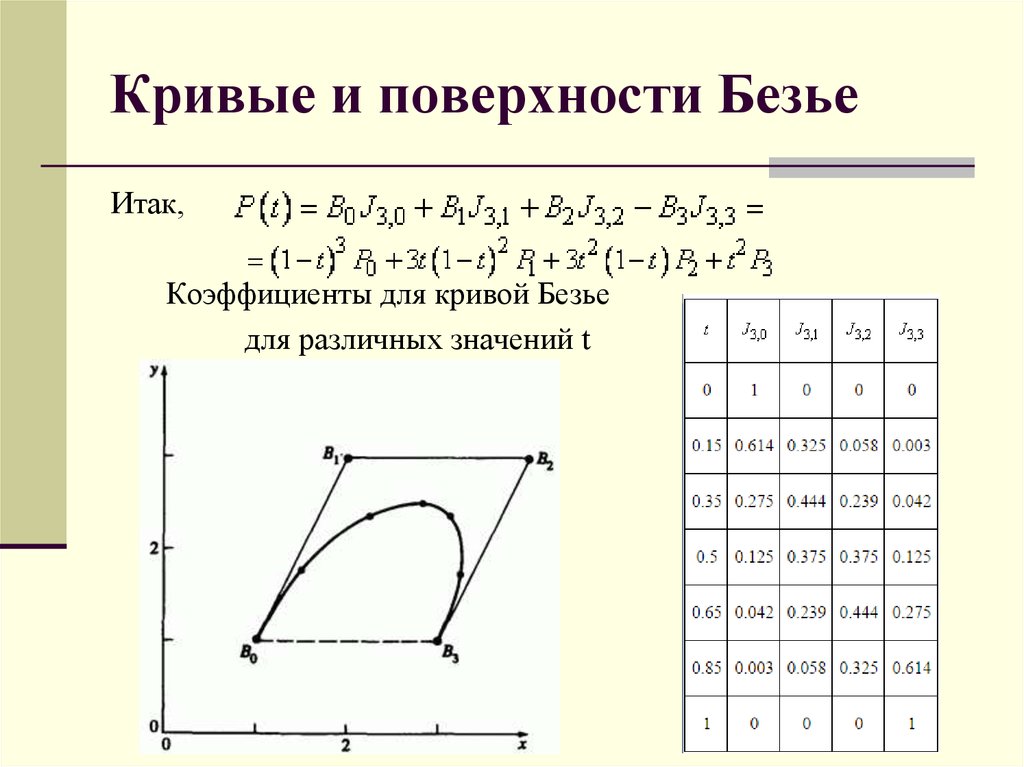
Ищу значение контрольной точки со знаком вопроса.
Я спрашиваю об этом, потому что хочу знать, как редакторы SVG архивируют что-то вроде:
Красная точка представляет значение, которое я ищу. Надеюсь, я имею смысл.
- математика
- графика
4
Квадратичная кривая Безье может быть лучше всего представлена алгоритмом Де Кастельжо. Таким образом, для данного t между 0 и 1 точка p на кривой определяется как: т*а + (1-т)*б
р между b и c : r = t*b + (1-t)*c r = t*q + (1-t)*r Итак, кривая Безье создается путем интерполяции между точками, которые, в свою очередь, также интерполируются. (Обратите внимание, что в отличие от первого изображения, ваше второе изображение не использует одно и то же t для трех интерполяций.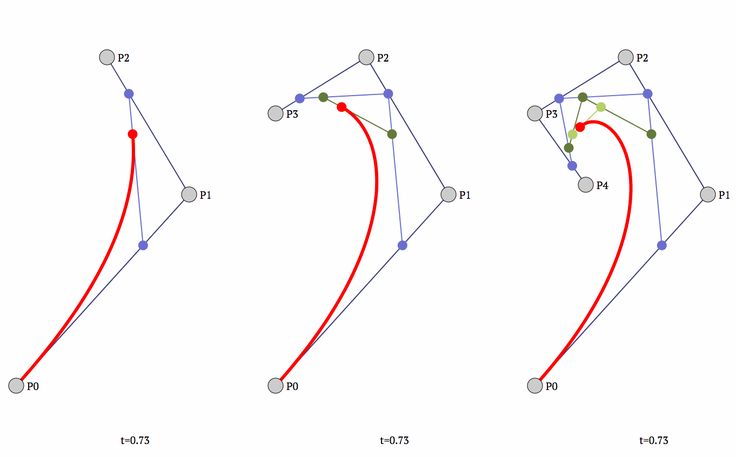

 1*(5;0) = (0.5; 0)
1*(5;0) = (0.5; 0) 2*(0;0) + 0.8*(5;0) = (4; 0)
2*(0;0) + 0.8*(5;0) = (4; 0)
 Хуже всего дела по поддержке формата SVG у Microsoft, которая покинула группу 2003 г. Для Internet Explorer – необходим Adobe SVG Viewer (ASV). С 9 версии IE частично поддерживает функции SVG.
Хуже всего дела по поддержке формата SVG у Microsoft, которая покинула группу 2003 г. Для Internet Explorer – необходим Adobe SVG Viewer (ASV). С 9 версии IE частично поддерживает функции SVG. roots (dcoeffs)
roots (dcoeffs)