Соотношение золотого сечения в цифрах: Что такое золотое сечение и правда ли оно повсюду |

Содержание

Что такое золотое сечение и правда ли оно повсюду

18 июля 2021ЛикбезЖизнь

Спойлер: это лишь красивая математическая легенда.

Что такое золотое сечение

Это соотношение двух неравных чисел, при котором большее так же относится к меньшему, как сумма этих чисел к большему. Золотое сечение равно примерно 1,618, или 1,62, если округлить, и обозначается греческой буквой φ, «фи» — от имени древнегреческого скульптора Фидия. Считается, что он использовал такие пропорции при оформлении Парфенона.

Наиболее известные графические представления золотого сечения — это прямоугольник с соотношением сторон примерно 62:48 и построенная в нём спираль.

1 / 0

«Золотой прямоугольник» можно разделить на такие же, только меньшего размера. Изображение: Dicklyon / Wikimedia Commons

2 / 0

«Золотая спираль» (красная), вписанная в «золотой прямоугольник». Изображение: Silverhammermba & Jahobr / Wikimedia Commons

Золотое сечение тесно связано с числами Фибоначчи. Это ряд чисел, каждое из которых равняется сумме двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Чем дальше продолжается этот ряд, тем ближе соотношение соседних чисел в нём к 1,618. Например, 3/2=1,5; 8/5=1,6, а 34/21= 1,619.

Почему золотое сечение так популярно

Впервые им заинтересовались ещё древнегреческие математики Пифагор и Евклид. Они считали, что на числах построено всё мироздание и с их помощью можно объяснить любой феномен. Неудивительно, что элегантное соотношение так заинтересовало античных мыслителей.

Вслед за ними золотым сечением увлеклись многие выдающиеся учёные и деятели искусства. Например, Леонардо да Винчи, Альбрехт Дюрер, Иоганн Кеплер, Ле Корбюзье, Сальвадор Дали и Ричард Пенроуз.

Его считают «божественной пропорцией»

Название «золотое сечение» придумал немецкий математик XIX века Мартин Ом. До него это соотношение именовали «божественной пропорцией».

Из‑за приписываемых характеристик золотое сечение старались применять как можно чаще.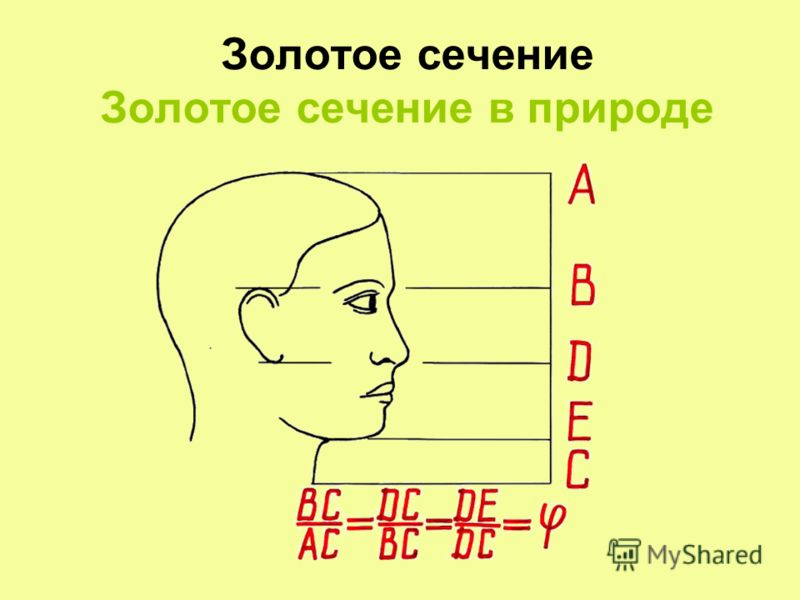 Так, во времена Возрождения это число считалось идеальным способом для выбора размера. «Золотой прямоугольник», например, нередко использовали при создании книг и картин. А линию пояса называли границей золотого сечения человеческого тела.

Некоторые и поныне считают эту пропорцию секретом привлекательности и примером универсальной гармонии, приятной человеческому глазу. Например, о золотом сечении любят говорить пластические хирурги. А ещё это число популярно как никакое другое в математике.

Его можно встретить в природе

Числа Фибоначчи и спирали, подобные золотому сечению, часто обнаруживаются в природе. Например, в количестве лепестков у цветов или форме растений.

Часть растения эониума. Фото: Max Ronnersjö / Wikimedia Commons

Его обнаруживают в произведениях архитектуры и искусства

Например, «божественные пропорции» находят в Парфеноне и египетских пирамидах. Также широко распространено заблуждение, что «Мона Лиза» написана в соответствии с числом φ.

Почему универсальность золотого сечения — миф

Однако при тщательном изучении становится понятно, что эта пропорция не так уж всеобъемлюща.

Божественность золотого сечения преувеличивается

Золотому сечению придают больше значения, чем есть в действительности. Красивые узоры и налёт таинственности сделали из обычного геометрического соотношения математический миф, который, к примеру, очень любят нумерологи.

Чаще всего вещи причисляют к золотому сечению с большими допущениями. Ни о какой точности и математической универсальности в таком случае говорить не приходится. Поэтому при желании можно обнаружить «божественные пропорции» где угодно.

В природе золотое сечение не так уж распространено

Его находят далеко не везде. Например, у маков всегда четыре лепестка, а в ряд Фибоначчи четвёрка не входит. Также нередко встречается четырёхлистный клевер. Раковины морских моллюсков похожи на спираль золотого сечения, но всё-таки другие. У них больше витков, и расстояние между ними меньше. Ни у одного моллюска коэффициент скручивания раковины и близко не равен 1,62. Это видно даже невооружённым глазом:

1 / 0

Спираль морского моллюска. Изображение: Florian Elias Rieser / Wikimedia Commons

2 / 0

Спираль Фибоначчи, близкая к золотому сечению. Изображение: Jahobr / Wikimedia Commons

В человеческом теле же столько точек, от которых можно производить измерение, что при желании реально найти золотое сечение где угодно. Вот только с большой вероятностью у разных людей «божественную пропорцию» придётся искать в разных местах, так как мы можем сильно отличаться друг от друга.

В искусстве оно тоже встречается не так уж часто

Изучение 565 картин выдающихся художников показало, что в среднем соотношение сторон в работах составляет 1,34. Это явно не дотягивает до золотого сечения. Учёные не находят его даже в произведениях Леонардо да Винчи.

Археологические исследования не подтверждают и того, что древние греки могли использовать золотое сечение при постройке Парфенона.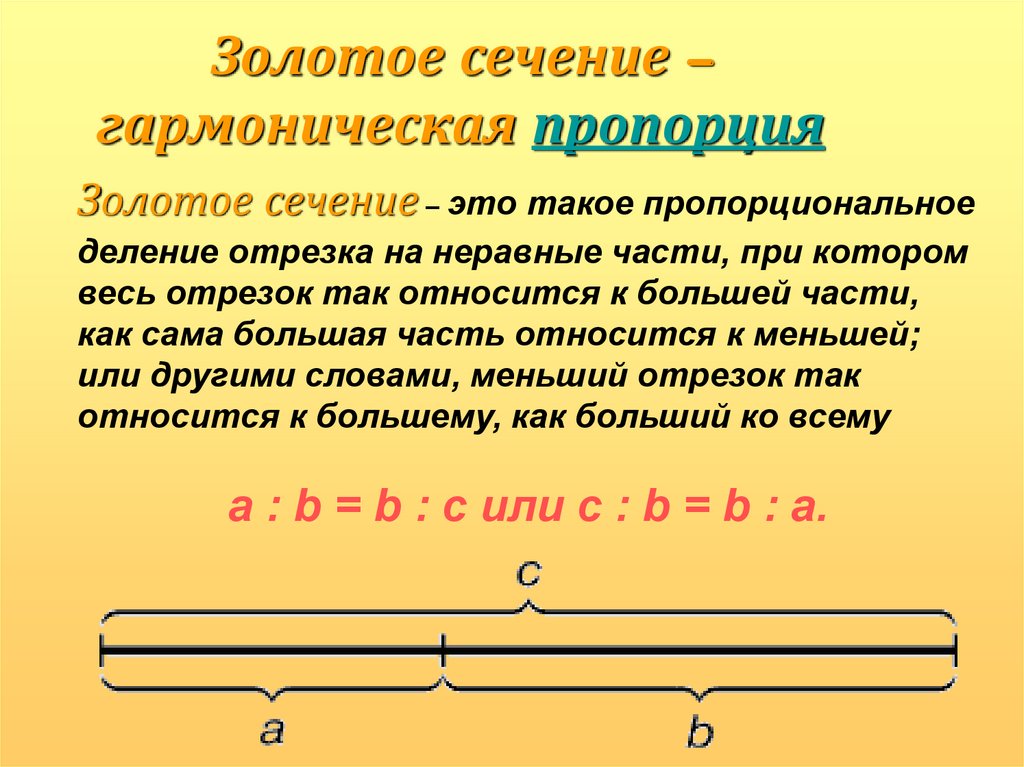 Из более чем 100 памятников древнегреческой архитектуры это число нашлось в пропорциях только четырёх объектов: башни, алтаря, гробницы и надгробия. Не могли пользоваться золотым сечением и древние египтяне, не обладавшие достаточным уровнем технологий, чтобы точно высчитывать пропорции.

Кому золотое сечение может быть полезно на самом деле

Современная математика использует золотое сечение и числа Фибоначчи при описании фракталов — фигур, которые проявляют самоподобие.

Фрактальная форма кочана капусты Романеско. Фото: Ivar Leidus / Wikimedia Commons

Знание о числе φ играет важную роль в изучении хаоса и изменяющихся (динамических) систем. Оно помогает понять, как природа развивается и самоорганизуется.

Также числа Фибоначчи полезны при решении некоторых сложных задач. Например, с помощью этих чисел советский математик Юрий Матиясевич доказал, что не существует универсального алгоритма решения уравнений с как минимум двумя неизвестными.

Читайте также 💆‍♂️👩‍🔬

Продолжите последовательность! 10 мини-задач для разминки мозга
Как округлять числа
Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
Гимнастика для ума: 10 увлекательных задач с числами
10 увлекательных задач от советского математика

Что такое «золотое сечение»?.

На протяжении веков «золотое сечение»… | by Сергей Базанов | Paradox Review

На протяжении веков «золотое сечение» считается самым прекрасным соотношением в искусстве и архитектуре.

«Золотое сечение», называемое также «золотая пропорция» или «золотое соотношение», было обнаружено во многих самых знаменитых творениях человечества — от древнегреческого Парфенона до творений Сальвадора Дали. Возможно, вы уже читали на эту тему статью «Нереализованное влияние золотого сечения».

Не важно, считаете ли вы, что эта божественная пропорция является поистине знамением красоты или просто предвзятым выбором, но, без сомнения, это одно из самых интригующих чисел в мире. Поэтому, сейчас мы поговорим о математической основе «золотого сечения».

Впервые о «золотом сечении» упоминает древнегреческий математик Евклид около 300 лет до нашей эры. В шестой книге своего трактата «Начала» Евклид дает определение «золотого сечения». Он поручает нам взять отрезок линии и разделить его на два меньших сегмента так, что отношение всей линии (a + b) к отрезку a будет таким же, как отношение отрезка a к сегменту b:

Что эквивалентно пропорции:

Евклид использовал «золотое сечение» для построения правильного пятиугольника. Отношение диагонали правильного пятиугольника к его стороне равно золотому сечению. Правильный пятиугольник (пентагон) еще называют «золотой пятиугольник».

«Золотое сечение» часто представляют как «Золотой прямоугольник» — прямоугольник с отношением длин сторон примерно 1,618:1.

Этот прямоугольник обладает тем свойством, что если от него отрезать квадрат, то снова получится золотой прямоугольник меньшего размера и так до бесконечности.

Золотой прямоугольник.

На самом деле, соотношение сторон «золотого прямоугольника» — это иррациональное значение 1,618034…, т. е. бесконечная десятичная дробь, не имеющая периода.

Это число и есть пропорция «золотого сечения», оно обозначается греческой буквой Фи в честь древнегреческого скульптора и архитектора Фидия, мастера, воплотившего его в своих работах.

Чтобы найти значение 1,618034…, мы должны решить пропорцию, показанную выше. Для простоты предположим, что b = 1 и a = x и найдем решение для x.

a = x, b = 1

Шаг 1. Сделаем перекрестное умножение:

Шаг 2. Приведем уравнение к 0:

Шаг 3. Решим квадратное уравнение:

Поскольку мы работаем с длинами, нам нужно только положительное решение:

Решение найдено! «Золотое сечение» выражается, как дробь.
Для проверки подставим a = 1.618 и b = 1, чтобы убедиться, что наша пропорция верная:

Обратите внимание, как интересно: мы можем написать «золотое соотношение» при помощи самого себя. Это потрясающе!

Что эквивалентно:

Пойдем дальше… Заменим φ = 1 + 1 / φ для φ в знаменателе:

И еще дальше!

Мы могли бы продолжать делать это бесконечно. Оказывается, «Золотое сечение» может быть записано как бесконечная цепная дробь.

Мы можем использовать непрерывную дробь, чтобы раскрыть связь «золотого сечения» с последовательностью Фибоначчи.

Для начала мы немного изменим нашу бесконечную дробь — добавим индексы, чтобы показать, как следующее значение φ(n+1) может быть получено из предыдущего значения φ(n).

Так как это бесконечная цепная дробь, с ростом n искомое значение приближается к истинному значению φ.

Теперь допустим, что φ(0) = 1 и найдем φ(1).

Продолжим вычислять следующеезначение — φ(2)

И далее… φ(3), φ(4)…

Посмотрите! Это же последовательность Фибоначчи! Каждое приближение — это отношение двух соседних чисел Фибоначчи.

По мере продвижения к каждому новому последовательному вычислению мы обнаруживаем, что наше искомое значение все ближе и ближе приближается к его истинному «Золотому сечению».

На девятом члене последовательности Фибоначчи мы уже получаем значения «золотого сечения», с тремя верными цифрами после запятой.

В самом деле, limit F(n+1)/F(n) при n→∞ (где F(n) и F(n+1) представляют n и n+1 числа в последовательности Фибоначчи) сходится к φ.

Если визуализировать этот процесс, то мы увидим, как последовательность Фибоначчи создает прямоугольники всё ближе и ближе к «Золотому прямоугольнику».

Прямоугольник Фибоначчи.

Хотя в мире дизайна продолжаются споры о том, является ли «золотое сечение» оптимальной пропорцией или нет, можно с уверенностью сказать, что оно математически совершенно и не перестает нас удивлять.

What is the Golden Ratio?

You know you’re truly geeking out when you’re gushing about how beautiful a number is, but hey this number is pretty…

medium. com

Нереализованное влияние золотого сечения

Математика на службе у искусства

medium.com

Лучшая книга о Биткоине для начинающих

Всё, что вы хотели знать о Биткоине, но стеснялись спросить, найдете в книге «Биткоин для всех»

medium.com

золотое сечение | Примеры, определение и факты

золотое сечение

Просмотреть все материалы

Похожие темы:: игра в числа
пентаграмма
количество
иррациональное число
золотой прямоугольник

Просмотреть весь связанный контент →

золотое сечение , также известное как золотое сечение, золотое сечение или божественная пропорция , в математике иррациональное число (1 + квадратный корень из √5)/2, часто обозначаемое греческой буквой ϕ или τ, приблизительно равное 1,618. Это отношение отрезка, разрезанного на две части разной длины, так что отношение всего отрезка к более длинному отрезку равно отношению более длинного отрезка к более короткому отрезку. Происхождение этого числа можно проследить до Евклида, который упоминает его как «предельное и среднее отношение» в Элементах . С точки зрения современной алгебры, пусть длина более короткого отрезка равна одной единице, а длина более длинного отрезка равна 9.0023 x единиц дает уравнение ( x + 1)/ x = x /1; это можно преобразовать, чтобы сформировать квадратное уравнение x ² – x – 1 = 0, для которого положительное решение равно x = (1 + квадратный корень из √5)/2, золотое сечение.

Древние греки признавали это свойство «разделения» или «разделения», фраза, которая в конечном итоге была сокращена до просто «раздел». Более 2000 лет спустя и «отношение», и «сечение» были названы «золотыми» немецким математиком Мартином Омом в 1835 году. Греки также заметили, что золотое сечение обеспечивает наиболее эстетически приятную пропорцию сторон прямоугольника. , понятие, которое было усилено в эпоху Возрождения, например, работами итальянского эрудита Леонардо да Винчи и публикацией De divina пропорция (1509; Божественная пропорция ), написанная итальянским математиком Лукой Пачоли и проиллюстрированная Леонардо.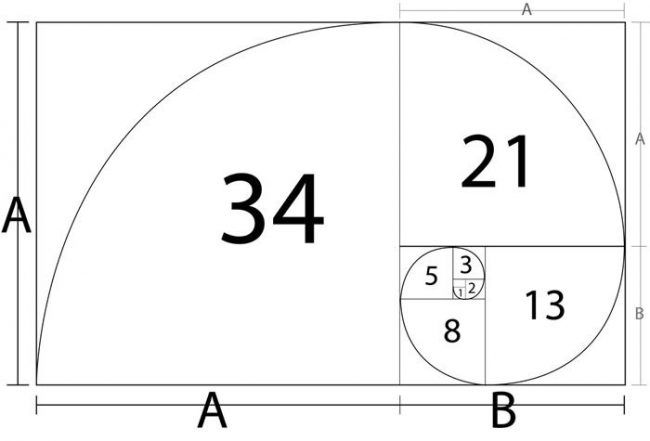

Britannica Quiz

Числа и математика

A-B-C, 1-2-3… Если вы считаете, что считать числа — это то же самое, что читать алфавит, проверьте, насколько свободно вы владеете языком математики в этом тесте.

Золотое сечение встречается во многих математических контекстах. Его геометрически можно построить с помощью линейки и циркуля, и он возникает при исследовании архимедовых и платоновых тел. Это предел соотношений последовательных членов последовательности чисел Фибоначчи 1, 1, 2, 3, 5, 8, 13,…, в которой каждый член после второго является суммой двух предыдущих, а также значение самой простой из цепных дробей, а именно 1 + 1/(1 + 1/(1 + 1/(1 +⋯, 9)0003

В современной математике золотое сечение встречается при описании фракталов, фигур, проявляющих самоподобие и играющих важную роль в изучении хаоса и динамических систем.

Стефан С. Карлсон

Золотое сечение – определение, формула, примеры

Золотое сечение, которое часто называют золотым сечением, божественной пропорцией или золотым сечением, представляет собой особый атрибут, обозначаемый символом ϕ, и примерно равен 1,618. Изучение многих специальных формаций может быть выполнено с использованием специальных последовательностей, таких как последовательность Фибоначчи, и атрибутов, таких как золотое сечение.

Это соотношение встречается в различных искусствах, архитектуре и дизайне. Многие замечательные архитектурные сооружения, такие как Великая пирамида Египта, Парфенон, были частично или полностью спроектированы так, чтобы отражать в своей структуре золотое сечение. Великие художники, такие как Леонардо да Винчи, использовали золотое сечение в нескольких своих шедеврах, и в 1500-х годах оно было известно как «Божественная пропорция». Давайте узнаем больше о золотом сечении в этом уроке.

1.	Что такое золотое сечение?
2.	Формула золотого сечения
3.	Как рассчитать золотое сечение?
4.	Что такое золотой прямоугольник?
5.	Что такое последовательность Фибоначчи?
6.	Часто задаваемые вопросы о золотом сечении

Что такое золотое сечение?

Золотое сечение, также называемое золотым сечением, божественной пропорцией или золотым сечением, существует между двумя величинами, если их отношение равно отношению их суммы к большей величине между ними. Со ссылкой на это определение, если мы разделим линию на две части, части будут в золотом сечении, если:

Отношение длины более длинной части, скажем, «а», к длине более короткой части, скажем, «b» равно отношению их суммы «(a + b)» к большей длине.

Обратитесь к следующей диаграмме для лучшего понимания вышеуказанной концепции:

Обозначается греческой буквой ϕ, произносимой как «фи». Приблизительное значение ϕ равно 1,61803398875 . Оно находит применение в геометрии, искусстве, архитектуре и других областях. Таким образом, следующее уравнение устанавливает соотношение для расчета золотого сечения: два.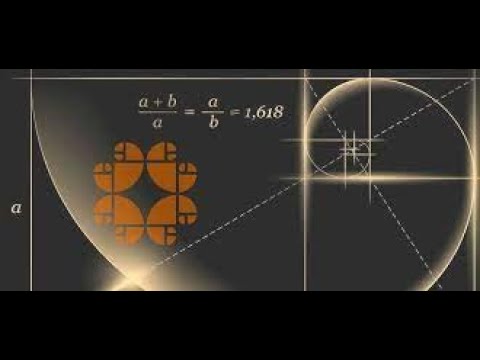

Определение золотого сечения

Когда линия делится на две части, длинная часть, которая делится на короткую часть, равна всей длине, деленной на длинную часть, определяется как золотое сечение. Ниже приведены примеры золотого сечения в архитектуре и искусстве.

Существует множество применений золотого сечения в области архитектуры. Многие архитектурные чудеса, такие как Великая мечеть Кайруана, были построены с учетом золотого сечения в их структуре. Такие художники, как Леонардо да Винчи, Рафаэль, Сандро Боттичелли и Жорж Сера, использовали это как атрибут в своих работах.

Формула золотого сечения

Формулу золотого сечения можно использовать для расчета значения золотого сечения. Уравнение золотого сечения выведено, чтобы найти общую формулу для расчета золотого сечения.

Уравнение золотого сечения

Из определения золотого сечения

a/b = (a + b)/a = ϕ

Из этого уравнения получаем два уравнения:

a/b = ϕ → ( 1)

(а + b)/а = ϕ → (2)

Из уравнения (1)

a/b = ϕ

⇒ a = b

Подставить это в уравнение (2):

(bϕ + b)/bϕ = ϕ

b( ϕ + 1)/ bϕ = ϕ

(ϕ + 1)/ϕ = ϕ

1 + 1/ϕ = ϕ

Как рассчитать золотое сечение?

Значение золотого сечения можно рассчитать разными методами. Начнем с основного.

Метод проб и ошибок

Мы угадаем произвольное значение константы, а затем выполним следующие шаги, чтобы вычислить более близкое значение на каждой итерации.

Вычислите мультипликативную обратную величину угаданного вами значения, т. е. 1/значение. Это значение будет нашим первым термином.
Вычислите другой член, добавив 1 к мультипликативному, обратному этому значению.
Оба условия, полученные на предыдущих шагах, должны быть равны. Если нет, мы будем повторять процесс, пока не получим примерно равное значение для обоих членов.
Для второй итерации мы будем использовать предполагаемое значение, равное члену 2, полученному на шаге 2, и так далее.

Например,

Поскольку ϕ = 1 + 1/ϕ, оно должно быть больше 1. Начнем со значения 1,5 в качестве нашего первого предположения.

Член 1 = Мультипликативное обратное 1,5 = 1/1,5 = 0,6666…
Член 2 = мультипликативный, обратный 1,5 + 1 = 0,6666. . + 1 = 1,6666…

Поскольку оба термина не равны, мы повторим этот процесс снова, используя предполагаемое значение, равное term 2 .

В следующей таблице приведены данные расчетов для всех принятых значений, пока мы не получим желаемые равные условия:

Итерация	Предполагаемое значение	Термин 1 (1/значение)	Термин 2 (1/значение + 1)
1.	1,5	11,511,5 = 0,6666..	0,6666.. + 1 = 1,6666..
2.	1.6666..	11,666..11,666.. = 0,6	0,6 + 1 = 1,6
3.	1,6	11,611,6 = 0,625	0,625 + 1 = 1,625
4.	1,625	11,62511,625 = 0,61538..	0,61538.. + 1 = 1,61538..
5.	1. 61538..	..	.. и так далее

Чем больше итераций вы выполните, тем ближе приблизительное значение будет к точному. Другие методы обеспечивают более эффективный способ вычисления точного значения. 92 — 4ac}}{2a}\)

Подставляя значения a = 1, b = -1 и c = -1, получаем

ϕ = \(\frac{1 \pm \sqrt{( 1 + 4 )}}{2}\)

Решение можно упростить до положительного значения, что даст:

ϕ = 1/2 + √5/2

Обратите внимание, что мы не рассматриваем отрицательное значение, так как \( \phi\) — это отношение длин, и оно не может быть отрицательным.

Следовательно, ϕ = 1/2 + √5/2

Что такое золотой прямоугольник?

В геометрии золотой прямоугольник определяется как прямоугольник, длины сторон которого находятся в золотом сечении. Золотой прямоугольник демонстрирует совершенно особую форму самоподобия. Все прямоугольники, созданные путем добавления или удаления квадрата, также являются золотыми прямоугольниками.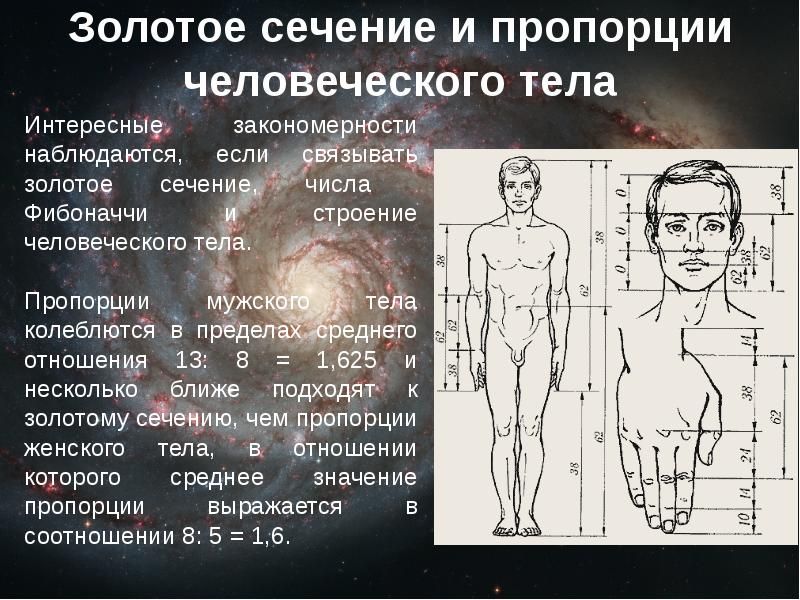

Построение золотого прямоугольника

Мы можем построить золотой прямоугольник, выполнив следующие действия:

Шаг 1: Сначала мы нарисуем квадрат со стороной 1 единица. На одной из его сторон нарисуйте точку посередине. Теперь мы проведем линию от этой точки до угла другой стороны.

Шаг 2: Используя эту линию в качестве радиуса и точку, проведенную посередине, в качестве центра, нарисуйте дугу, идущую вдоль стороны квадрата. Длину этой дуги можно рассчитать с помощью теоремы Пифагора: √(1/2) ² + (1) ² = √5/2 шт.
Шаг 3: Используйте пересечение этой дуги и стороны квадрата, чтобы нарисовать прямоугольник, как показано на рисунке ниже:

Это золотой прямоугольник, потому что его размеры находятся в золотом сечении. т. е. ϕ = (√5/2 + 1/2)/1 = 1,61803

Что такое последовательность Фибоначчи?

Последовательность Фибоначчи — это особый ряд чисел, в котором каждый член (начиная с третьего члена) является суммой двух предыдущих членов. Для нахождения последовательности Фибоначчи можно использовать следующие шаги:

Начнем с того, что возьмем 0 и 1 в качестве первых двух членов.
Таким образом, третий член 1 вычисляется путем сложения 0 и 1.
Точно так же следующий член = 1 + 2 = 3 и так далее.

Последовательность Фибоначчи задается как 0, 1, 1, 2, 3, 5, 8, 13, 21,… и так далее. Последовательность Фибоначчи и золотое сечение имеют между собой особую связь. Когда мы начинаем вычислять отношения двух последовательных членов ряда Фибоначчи, значение каждого последующего отношения становится ближе к точному значению ϕ.

Например,

В следующей таблице показаны значения соотношений, максимально приближающиеся к значению ϕ. В следующей таблице показаны значения соотношений, максимально приближающиеся к значению ϕ.

Срок 1	Срок 2	Соотношение = Клемма 2/ Клемма 1
2	3	1,5
3	5	1. 6666..
5	8	1,6
8	13	1,625
13	21	1,61538

☛Связанные темы

Ниже приведен список тем, тесно связанных с золотым сечением. Эти темы также дадут вам представление о том, как такие понятия рассматриваются в Cuemath.

Среднее
Соотношение
Числа Фибоначчи
Квадратные уравнения
Соотношение, доля, формулы процентов

Часто задаваемые вопросы о золотом сечении

Что такое золотое сечение простыми словами?

Золотое сечение — это математическое отношение, которое существует между двумя величинами, если их отношение равно отношению их суммы к большей из них величин. Другими словами, когда линия разделена на две части и более длинная часть «а», разделенная на меньшую часть «b», равна сумме (а + b), деленной на «а», это означает, что линия отражая золотое сечение, которое равно 1,618.

Что вы подразумеваете под золотым прямоугольником?

Почему золотое сечение красиво?

Золотое сечение — это соотношение, которое при использовании в различных областях для проектирования объектов делает объекты эстетически привлекательными и приятными на вид. Поэтому золотое сечение называют красивым атрибутом. Его можно заметить в различных узорах природы, например, в спиралевидном расположении цветов и листьев. Есть много применений золотого сечения в области архитектуры. Многие архитектурные чудеса были построены, чтобы отразить золотое сечение в своей структуре, например, Великая пирамида Египта и Великая мечеть Кайруана.

Почему золотое сечение важно?

Золотое сечение — это математическое соотношение, которое часто встречается в природе и используется в различных областях. Он используется в нашей повседневной жизни, искусстве и архитектуре. Объекты, созданные с учетом золотого сечения в своей структуре и дизайне, более приятны и эстетичны для глаз. Это можно заметить по спиралевидному расположению цветков и листьев.

Где в реальной жизни используется золотое сечение?

Существует множество применений золотого сечения в области искусства и архитектуры. Многие архитектурные чудеса были построены, чтобы отразить золотое сечение в своей структуре. Такие художники, как Лео да Винчи, Рафаэль, Сандро Боттичелли и Жорж Сера, использовали это как атрибут в своих работах. Его можно использовать для изучения структуры многих объектов в нашей повседневной жизни, которые напоминают определенный узор.

Кто открыл золотое сечение?

Древнегреческие математики первыми упомянули золотое сечение в своих работах. Математики V века до нашей эры Гиппакус и Евклид внесли большой вклад в свои исследования по этому вопросу.

Что такое формула золотого сечения?

Формулу золотого сечения можно использовать для расчета значения золотого сечения.