2+3
Не всегда можно определить заранее, сколько раз придется вычислять функцию. Метод золотого сечения почти столь же эффективен при n-2, что и метод Фибоначчи, однако при этом не требуется знать n – количество вычислений функции.
Сущность этого метода заключается в следующем. Интервал неопределенности делится на две неравные части так, что отношение длины большего отрезка к длине всего интервала равно отношению длины меньшего отрезка к длине большего (рис 3).
где τ — «золотое сечение»
На каждом шаге этой итеративной процедуры, кроме первого, вычисляется только одно значение функции. Однако Химмельблау рекомендовал вычислять на каждом шаге две точки, для того чтобы не накапливалась погрешность, так как τ имеет приближенное значение (рис 4).
Если длина конечного интервала неопределенности равна δ, то для достижения требуемой точности число вычислений значений функции по методу золотого сечения можно найти по условию
Пример.
Методом золотого сечения найти точку минимума x* функции f(x) на отрезке [a;b] с точностью ε и значение целевой функции в этой точке:
f(x)=x4+2x2+4x+1=0, [-1;0], ε=0.1
Решение. Положим a1 = a, b1 = b. Вычислим λ1 = a1 + (1- 0.618)(b1 — a1), μ1 = a1 + 0.618(b1 — a1).
Вычислим f(λ1) = -0.5623, f(μ2) = -0.2149
Итерация №1.
Поскольку f(λ1) 1), то b2 = -0.382, a2 = a1, μ2 = -0.618
μ2 = a2 + 0.618(b2 — a2) = -1 + 0.618(-0.382 +1), f(μ2) = f(-0.618) = -0.2149
Итерация №2.
Поскольку f(λ2) > f(μ2), то a3 = -0.7639, b3 = b2, λ3 = -0.618
μ3 = a3 + 0.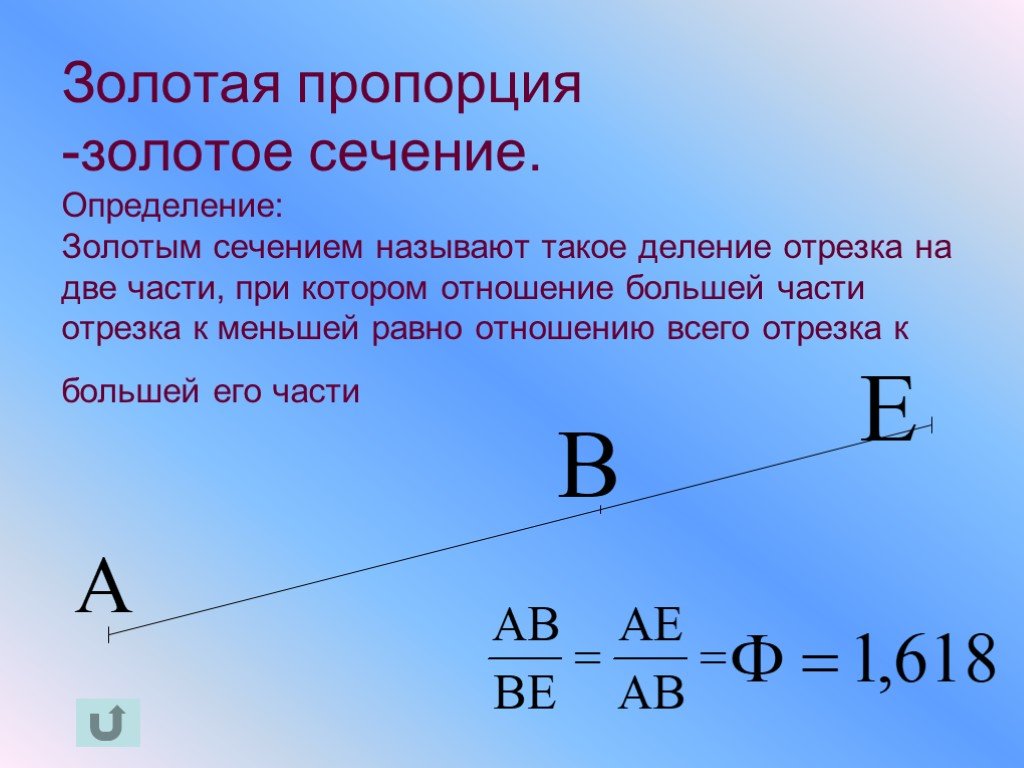
618(b3 — a3) = -0.7639 + 0.618(-0.382 +0.7639), f(μ3) = f(-0.5279) = -0.5623
Итерация №3.
Поскольку f(λ3) 3), то b4 = -0.5279, a4 = a3, μ4 = -0.618
μ4 = a4 + 0.618(b4 — a4) = -0.7639 + 0.618(-0.5279 +0.7639), f(μ4) = f(-0.618) = -0.4766
Итерация №4.
Поскольку f(λ4) 4), то b5 = -0.618, a5 = a4, μ5 = -0.6738
μ5 = a5 + 0.618(b5 — a5) = -0.7639 + 0.618(-0.618 +0.7639), f(μ5) = f(-0.6738) = -0.5623
Остальные расчеты сведем в таблицу.
| N | an | bn | bn-an | λn | μn | F(λn) | F(μn) |
| 1 | -1 | 0 | 1 | -0. 618 | -0.382 | -0.5623 | -0.2149 |
| 2 | -1 | -0.382 | 0.618 | -0.7639 | -0.618 | -0.548 | -0.5623 |
| 3 | -0.7639 | -0.382 | 0.3819 | -0.618 | -0.5279 | -0.5623 | -0.4766 |
| 4 | -0.7639 | -0.5279 | 0.236 | -0.6738 | -0.618 | -0.5811 | -0.5623 |
| 5 | -0.7639 | -0.618 | 0.1459 | -0. 7082 | -0.6738 | -0.5782 | -0.5811 |
| 6 | -0.7082 | -0.618 | 0.09018 | -0.6738 | -0.6524 | -0.5811 | -0.5772 |
Находим x как середину интервала [a,b]: x=(-0.618-0.70818104)/2 = -0.66309052.
Ответ: x = -0.66309052; F(x) = -0.57965758
Содержание
3. Метод золотого сечения
Одним
из наиболее эффективных методов, в
которых при ограниченном количестве
вычислений f(x) достигается наилучшая
точность, является метод золотого
сечения. Он состоит в построении
последовательности отрезков
[ао,Ьо],[a1,b1],…
, стягивающихся к точке минимума функции
f(x). На каждом шаге, за исключением
первого, вычисление значения функции
f(x) проводится лишь в одной точке. Эта
точка, называемая золотым сечением.
Идея
метода(геометрически)
Внутри
отрезка [ао,bо]
выбираем некоторые внутренние точки
х1 и Х2 и вычисляем значения целевой
функции f(x1) и f(x2).
Поскольку f(x1)
< f(x2), очевидно, что минимум расположен
на одном из прилегающих к х1 отрезков:
[ao,x1]
или [x1,x2]. Поэтому отрезок [x2,Ьо]
можно отбросить, сузив тем самым
первоначальный интервал неопределённости.
Далее
проводим на отрезке [а1, b1]
где а1 = а0, Ь1 = = Х2. Нужно снова выбрать
две внутренние точки, но одна из них
(х1) осталась из предыдущего шага, поэтому
достаточно выбрать лишь одну точку х3,
вычислить значение f(x3)
и провести сравнение.
f(х3)
< f(x1),
значит минимум находится на отрезке
[x3,
b1].
Обозначим
этот
отрезок [a2,b2],
снова выберем одну внутреннюю точку и
повторим процедуру сужения интервала
неопределенности. Процесс оптимизации
повторяется до тех пор, пока длина
очередного отрезка [ak,bk]
не станет меньше заданной величины е.
Способ
размещения внутренних точек на каждом
отрезке.
Пусть
длина интервала неопределенности равна
l,
а точка деления разбивает его на части
l1, l2:
l1
> l2,
I = l1
+ l2.
Золотое сечение интервала неопределенности
выбирается так, чтобы отношение длины
большего отрезка к длине всего интервала
равнялось отношению длины меньшего
отрезка к длине большего отрезка:
Преобразуем
это выражение и найдем значения
Интервал
неопределенности можно разделить в
соотношении золотого сечения двояко:
в пропорциях I2 : l1
и l1 : l2.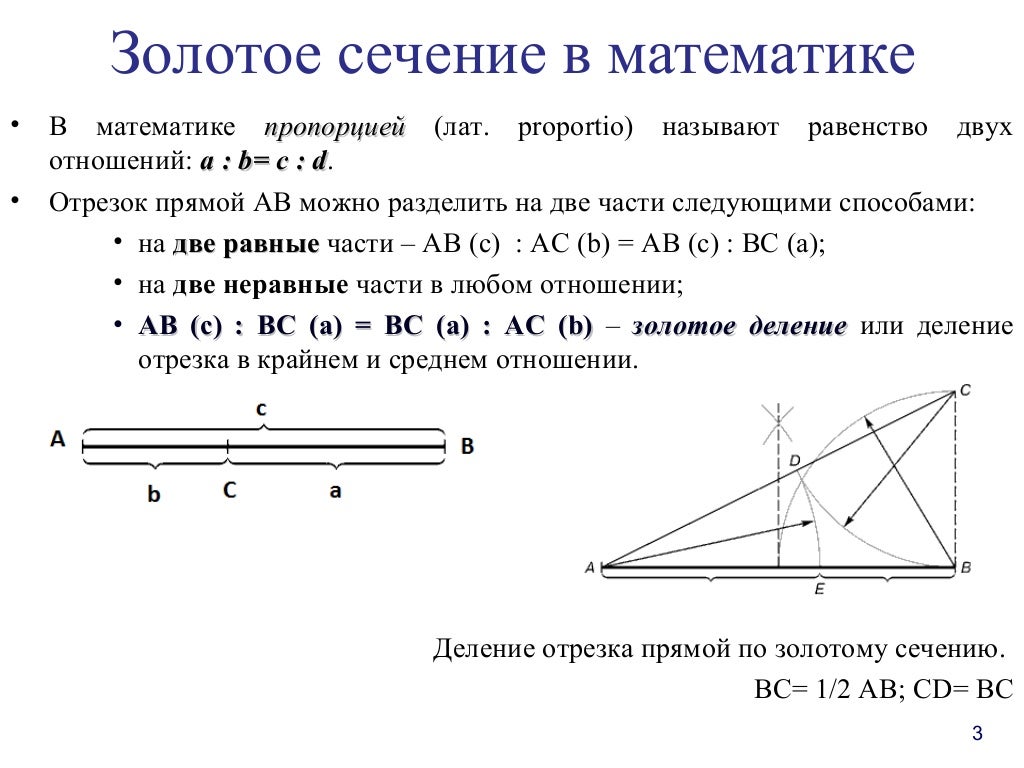
Имеем:
Алгоритм
процесса одномерной оптимизации методом
золотого сечения:
4. Метод Ньютона
Пусть
х = с — решение уравнения f’(x),
а с0 — некоторое начальное приближение
к с. Применим метод Ньютона решения
уравнения F(x) = 0, которое эквивалентно
уравнению при F(x) =f’
(х). Для этого в формулу для к-то приближения
метода Ньютона подставим вместо F(x)
производную f'(x) и получим тем самым
формулу для к-то приближения к решению
уравнения:
Для
использования этой формулы необходимо,
чтобы:
Достаточные
условия сходимости метода Ньютона:
последовательность
значений
Точка
x=c
может являться и точкой минимума, и
точкой максимума, а может вообще не
являться точкой экстремума.
Метод
Ньютона обладает более быстрой
сходимостью, чем методы, которые не
используют дифференциальные свойства
функции. Но сходимость не гарантирована,
если не удачно выбрать начальное
приближение.
Пример.
23.
Метод покоординатного спуска.
Метод
покоординатного спуска сводит задачу
о нахождении наименьшего значения
функции многих переменных к многократному
спуску в сторону уменьшения значений
функции по каждому проектному параметру.
Данный метод легко проиллюстрировать
геометрически для случая функции двух
переменных z = f(x,y), описывающей некоторую
поверхность в трехмерном пространстве.
Процесс
оптимизации в этом случае проходит
следующим образом. Точка М0(x0,y0)
описывает начальное приближение. Проводя
спуск по координате х, попадем в точку
M1(x1,y0). Далее, двигаясь параллельно оси
ординат, придем в точку М2(x1,y1)
и т. д.
Для
функции двух переменных очевидно, что
метод может оказаться неприменимым при
наличии изломов в линиях уровня. Для
гладких функций при удачно выбранном
начальном приближении (в некоторой
окрестности минимума) процесс сходится
к минимуму. Здесь однако применение
метода затруднено в случае так называемых
оврагов на поверхности.
2. Точкой минимума этой функции
является начало координат. Наличие
оврага приводит к тому, что процесс
спуска к минимуму очень длительный,
метод сходится медленно. Так при начальном
приближении х = у = 1.5 после 50 итераций
получается приближение х~ у ~ 0.006.
К
достоинствам метода покоординатного
спуска следует отнести возможность
использования простых алгоритмов
одномерной оптимизации. Структурограмма
метода покоординатного спуска представлена
на
рисунке:
Итерации
завершаются при выполнении условия:
Золотое сечение — применение, история, типы, примеры и часто задаваемые вопросы
Золотое сечение, в математике также известное как золотое сечение, божественная пропорция или золотое сечение, представляет собой иррациональное число, которое обозначается греческой буквой «фи». или «ф». Золотое сечение или золотое число определяется как отношение отрезка прямой, который разрезается на две части неравной длины, где отношение всего отрезка к самому длинному отрезку равно отношению более длинного отрезка к более короткому отрезку.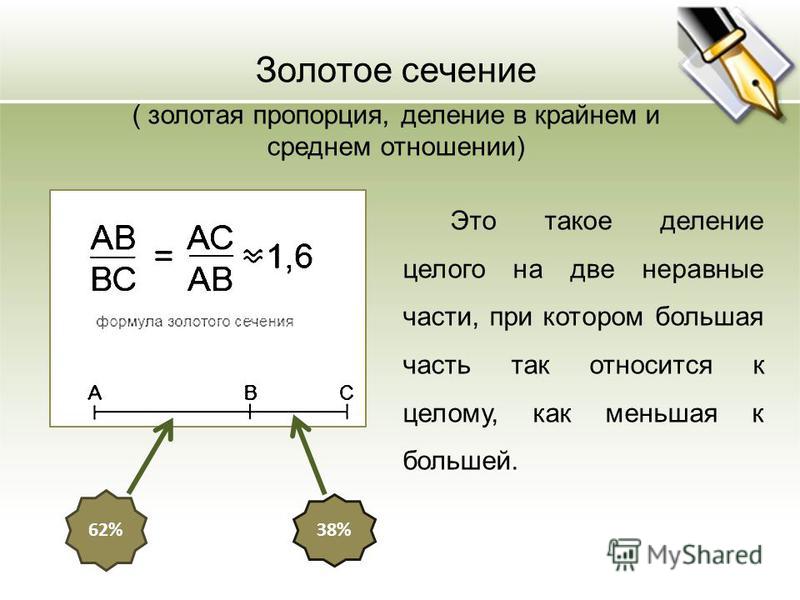
. Значение золотого сечения или золотое число — это иррациональное число \[\frac{(1+\sqrt{5})}{2}\] , которое приблизительно равно 1,618.
История золотого сечения
История золотого сечения восходит к древним временам, когда греческие математики, такие как Евклид и Пифагор, проводили бесконечные часы, исследуя уравнение и его свойства. Греческий математик Евклид упоминает о золотом сечении в элементах, где он реализовал некоторые положения соотношения. Он называл это крайним и средним соотношением.
Золотое сечение часто фигурировало в геометрических расчетах, включая пентаграммы и пятиугольники. Древний математик Гиппас V века до н.э. обнаружил, что золотое число или божественная пропорция не является ни целым числом, ни дробью, что удивило пифагорейцев.
За последние десятилетия многие математики изучали важность, использование и свойства золотого числа и применяли его ко многим математическим формулам и вычислениям.
В 18 веке математики, в том числе Абрахам де Муавр, Даниэль Бернулли и Леонард Эйлер, использовали формулу золотого сечения для определения значения чисел Фибоначчи. В 1960-х годах Стив Бэр открыл систему построения Zome, основанную на формуле золотого сечения.
Применение и использование Золотого сечения
Золотое сечение может применяться в различных областях науки, от искусства и архитектуры до природы. Ниже приведены некоторые из наиболее важных применений божественной пропорции.
Искусство: Большинство живописцев и художников использовали золотое сечение в своих художественных шедеврах в античную эпоху. Они использовали соотношение, чтобы добавить красоты и сделать свое искусство идеальным. Такие математики, как Лука Пачоли, использовали золотое сечение, чтобы обеспечить приятные и гармоничные пропорции для картин. Он также нашел католическое религиозное значение в соотношении, в связи с чем он также назвал картины в честь соотношения.
Другой великий художник, Леонардо да Винчи, также использовал золотое сечение Пачоли в своих картинах, чтобы выявить в них идеальные пропорции. Знаменитая картина Леонардо да Винчи «Мона Лиза» основана на золотом сечении и считается самой красивой картиной с идеальными пропорциями лица.
Рисунки и книги: В книгах ранних веков можно найти божественную пропорцию, которая находится в соотношении 5:3 и встречается редко. Божественную пропорцию мы можем найти во многих древних рукописях и инкунабулах, напечатанных в европейских странах. Даже сегодня вы также можете найти золотое сечение во многих дизайнах, включая игральные карты, плакаты, открытки, выключатели и телевизоры.
Музыка: Золотое сечение также играет решающую роль в музыкальной индустрии, и многие известные композиторы и певцы используют его в своих музыкальных шедеврах. Известный французский композитор Эрик Сати использовал золотое сечение в нескольких своих песнях, в том числе в Sonneries de la Rose.
Природа: Мы также можем наблюдать золотое сечение в различных аспектах природы. Согласно Иоганну Кеплеру, золотое сечение в природе можно увидеть в размножении растений и порождающих актах животных.
Многие другие ученые и исследователи нашли доказательства существования золотого сечения в естественной деятельности, утверждая, что это универсальный закон природы.
Помимо областей, упомянутых выше, золотое сечение также используется для изучения идеальных пропорций лица. По мнению ученых, люди с золотым сечением лица считаются более красивыми и привлекательными, чем другие. Они считают, что между всеми чертами лица должен быть пропорциональный разрыв, чтобы человек выглядел привлекательно.
Калькулятор золотого сечения
Калькулятор золотого сечения — это ценный, но простой метод расчета, который помогает определить более короткий отрезок, более длинный отрезок и суммарное значение отрезка с помощью простой формулы.
Если мы рассмотрим отрезок прямой с более длинным отрезком a и более коротким отрезком b, золотое сечение можно рассчитать по формуле: (a+b)/a = a/b.
Вы можете легко рассчитать золотое сечение любых двух величин вручную; вот шаги:
Сначала выберите большую сторону или значение и обозначьте ее как «а».
Снова возьмите меньшую сторону или значение и обозначьте его как «b».
Теперь введите все значения по формуле; (а+б)/а = а/б.
Вычислить a+b и разделить результат на значение a.
Расчет a/b.
Если ответ примерно равен 1,618, то ваши количества находятся в золотой пропорции.
Что такое прямоугольник золотого сечения?
Изучая концепции золотого сечения, мы часто сталкиваемся с термином прямоугольник золотого сечения, но что это такое? Давай выясним. Прямоугольник золотого сечения или золотой прямоугольник — это прямоугольник, длина которого обозначается как a+b, а ширина обозначается как a. Здесь а — более длинная сторона, а b — более короткая. Он используется в искусстве и архитектуре для создания идеальных пропорций в конструкциях и картинах.
Факты и примеры золотого сечения
Выше мы обсуждали золотое сечение, его применение и расчет; теперь давайте обсудим некоторые примеры золотого сечения и рассмотрим некоторые удивительные факты о золотом сечении.
Ниже приведены несколько примеров золотого сечения, которые помогут вам понять концепцию золотого числа.
Вы можете найти образец золотого сечения в архитектурных чудесах, таких как Великая пирамида Гизы.
Вы также можете найти золотое сечение в знаменитой картине Моны Лизы Леонардо да Винчи.
Вы также можете найти золотое сечение в лепестках цветов.
Лепестки цветка всегда следуют ряду Фибоначчи, тесно связанному с золотым сечением.Спиральная форма галактики является прекрасным примером золотого сечения, где каждый спиральный рукав составляет примерно 12 градусов.
(изображение скоро будет обновлено)
Вот несколько фантастических и удивительных фактов о золотом сечении.
Золотое сечение имеет много названий, включая золотое сечение, золотую пропорцию, божественную пропорцию, срединное сечение, крайнее и среднее отношение и т. д.
Золотое сечение встречается только тогда, когда формула уравнения равна к числу фи, равному 1,618.
Мы можем найти золотое сечение в вещах вокруг нас, и многие формы природы также доказывают, что золотое сечение является универсальным законом.
Значение золотого сечения представляет собой непрерывную дробь, поэтому оно обозначается символом «фи».
Золотое сечение – объяснение и примеры
Золотое сечение – это интригующее математическое соотношение между двумя величинами. Более того, это интересная концепция математически и с эстетической, а иногда и с метафизической точки зрения.
Две величины $a$ и $b$ с $a > b$ называются пропорциями золотого сечения, если $\dfrac{ a + b}{a} = \dfrac{a}{b}$
Отношение $\frac{a}{b}$ также обозначается греческой буквой $\Phi$, и мы можем показать, что оно равно $\frac{1 + \sqrt{5}}{2 } \примерно 1,618$. Обратите внимание, что золотое сечение является иррациональным числом, т. е. числа с десятичной точкой продолжаются вечно без какого-либо повторяющегося шаблона, и мы используем $1,618$ только в качестве приблизительного значения. Некоторые другие названия золотого сечения — золотая середина, золотое сечение и божественная пропорция.
Что такое золотое сечение:
Золотое сечение легко понять на примере палочки, которую мы ломаем на две неравные части $a$ и $b$, где $a>b$, как показано на рисунке ниже
Есть много способов разломить палку на две части; однако, если мы разобьем его определенным образом, т. е. отношение длинной части ($a$) и короткой части ($b$) также будет равно отношению общей длины ($a + b$) и длинная часть ($a$), то говорят, что $a$ и $b$ находятся в золотом сечении. На рисунке ниже показан пример, когда две части палочки находятся в золотом сечении, а когда нет.
Расчет золотого сечения:
Выше мы говорили, что золотое сечение в точности равно $\frac{1 + \sqrt{5}}{2}$. Откуда это число? Мы опишем два метода нахождения значения $\Phi$. Во-первых, мы начнем с определения, что $a$ и $b$ находятся в золотом сечении, если
$\frac{a}{b} = \frac{a + b}{a} = 1 + \frac{b}{a}$
Пусть $\Phi = \frac{a}{b}$ тогда $\frac{b}{a} = \frac{1}{\Phi}$, поэтому приведенное выше уравнение принимает вид
$\Phi = 1 + \frac{1}{\Phi}$.
Метод-1: Рекурсивный метод
Мы принимаем любое значение для $\Phi$, скажем, мы предполагаем, что $\Phi=1.2$. Теперь подставим это значение в приведенную выше формулу, т. е. $\Phi = 1 + \frac{1}{\Phi}$, и получим новое значение $\Phi$ следующим образом:
$\Phi = 1 + \ гидроразрыва {1} {1,2} = 1,8333 $.
Теперь мы снова подставляем это новое значение в формулу золотого сечения, чтобы получить другое значение, то есть
$\Phi = 1 + \frac{1}{1.8.3333} = 1,54545$.
Если мы будем продолжать повторять этот процесс, мы все ближе и ближе будем приближаться к действительному значению $\Phi$. As we show in the table below
Value | 1 + 1/Value | |||||||||||||||||||
1.2 | 1.8333 | |||||||||||||||||||
1.8333 | 1.5454 | |||||||||||||||||||
1.5454 | 1.647 | |||||||||||||||||||
1.647 | 1.607 | |||||||||||||||||||
1.607 | 1.622 | |||||||||||||||||||
1.622 Квадратичная формула2 + \beta x + c = 0$, и учитывая, что $x=\Phi$, $\alpha=1$, $\beta=-1$ и $c=-1$, получаем $\Phi = \frac{1 \pm \sqrt{1- 4 \times 1 \times -1}}{2} = \frac{1 \pm \sqrt{5}}{2}$. Квадратное уравнение всегда имеет два решения, в данном случае одно решение, т. е. $\frac{1 + \sqrt{5}}{2}$, положительно, а второе решение, т.е. $\frac{1 – \sqrt{5}}{2}$ является отрицательным. Поскольку мы считаем $\Phi$ отношением двух положительных величин, значение $\Phi$ равно $\frac{1 + \sqrt{5}}{2}$, что примерно равно 1,618. . 92 = 1 + \Phi$. Примеры золотого сечения:Есть много интересных математических и природных явлений, где мы можем наблюдать золотое сечение. Мы опишем некоторые из них ниже. Первое число Фибоначчи равно 0, а второе — 1. После этого каждое новое число Фибоначчи создается путем сложения двух предыдущих чисел. Например, мы можем записать третье число Фибоначчи, сложив первое и второе числа Фибоначчи, т. е. 0 + 1 = 1. Точно так же мы можем записать четвертое число Фибоначчи, сложив второе и третье числа Фибоначчи, т. е. 1+. 1 = 2 и т. д. Последовательность чисел Фибоначчи называется последовательностью Фибоначчи и показана ниже: $0, \,\, 1, \,\, 1, \,\, 2,\,\, 3,\,\, 5,\,\, 8,\,\, 13,\,\, 21,\,\, 34, \cdots$ Если мы начнем делить последующие числа Фибоначчи, результаты все ближе и ближе будут приближаться к золотому сечению, как показано в таблице ниже:
Золотое сечение в геометрииПятиугольник и пентаграммаЗолотое сечение часто встречается в правильном пятиугольнике и связанной с ним пентаграмме. Рисуем правильный пятиугольник на рисунке ниже. Если соединить вершины пятиугольника, то получится звездообразная геометрическая фигура внутри, которая называется пентаграммой, показанной ниже Многие линии подчиняются золотому сечению на приведенном выше рисунке. $\frac{DE}{EF}$ находится в золотом сечении $\frac{EF}{FG}$ находится в золотом сечении $\frac{EG}{EF}$ находится в золотом сечении $\frac{BE}{AE}$ находится в золотом сечении, $\frac{CF}{GF}$ находится в золотом сечении, и многие другие. Золотая спиральВозьмем прямоугольник, одна сторона которого равна 1, а другая равна $\Phi$. Отношение большой стороны к меньшей равно $\frac{\Phi}{1}$. Мы показываем прямоугольник на рисунке ниже. Теперь допустим, что мы делим прямоугольник на квадрат, все стороны которого равны 1, и меньший прямоугольник, одна сторона которого равна 1, а другая равна $\Phi-1$. Теперь отношение большей стороны к меньшей равно $\frac{1}{\Phi-1}$. Новый прямоугольник нарисован синим цветом на рисунке ниже 9.2 -\Phi -1 = 0$, мы можем переписать его как $\Phi(\Phi -1) = 1$ или $\frac{\Phi}{1} = \frac{1}{ \Phi -1}$ Следовательно, новый прямоугольник синего цвета имеет то же отношение большой стороны к меньшей, что и исходный прямоугольник. Если мы соединим точки, которые делят прямоугольники на квадраты, мы получим спираль, называемую золотой спиралью, как показано ниже. 92$, Если начертить прямоугольный треугольник с гипотенузой, равной $\Phi$, основанием, равным $\sqrt{\Phi}$, и перпендикуляром, равным 1, то это будет прямоугольный треугольник. Такой треугольник называется треугольником Келпера, и мы показываем его ниже: Золотое сечение в природе Существует множество природных явлений, где золотое сечение проявляется довольно неожиданно. Наиболее легко наблюдать спиралевидную структуру и последовательность Фибоначчи, встречающиеся в различных деревьях и цветах. Например, во многих случаях листья на стебле растения растут по спирали, по спирали, и если мы посчитаем количество витков и количество листьев, мы обычно получим число Фибоначчи. Также утверждается, что идеальное или совершенное человеческое лицо соответствует золотому сечению. Но, опять же, это очень субъективно, и нет единого мнения о том, что представляет собой идеальное человеческое лицо. Кроме того, все типы соотношений можно найти на любом человеческом лице. В человеческом теле отношение высоты морского к общему росту также близко к золотому сечению. Тем не менее, опять же, мы должны помнить, что в человеческом теле можно найти множество соотношений между 1 и 2, и если мы перечислим их все, то некоторые из них обязательно будут близки к золотому сечению, а другие будут совсем не такими. Наконец, спиралевидная структура рукавов галактики и раковины наутилуса также цитируются как примеры золотого сечения в природе. Какая часть золотого сечения на самом деле присутствует в природе и сколько мы навязываем природе, является субъективным и противоречивым. Мы оставляем этот вопрос на усмотрение читателя. Золотое сечение в архитектуре и дизайнеМногие люди считают, что золотое сечение эстетично, и художественные проекты должны следовать золотому сечению. Также утверждается, что золотое сечение много раз появлялось на протяжении веков при проектировании известных зданий и шедевров искусства. Например, , Золотое сечение много раз встречается в знаменитых колоннах Парфенона. Точно так же утверждается, что пирамиды Гизы также содержат золотое сечение как основу своего дизайна. Некоторыми другими примерами являются Тадж-Махал и Нотр-Дам и т. д. Однако следует помнить, что мы не можем достичь идеального золотого сечения, поскольку это иррациональное число. Однако некоторые современные здания, такие как здания Секретариата Организации Объединенных Наций, на самом деле были спроектированы с использованием системы, основанной на золотых пропорциях. Точно так же считается, что Леонардо Ди Винчи в значительной степени полагался на использование золотого сечения в своих работах, таких как «Мона Лиза» и «Витрувианский человек». Является ли золотое сечение действительно эстетичным и должно ли оно быть включено в дизайн архитектуры и искусства, это вопрос субъективный, и мы оставляем этот вопрос на усмотрение читателя. Если вы действительно заинтересованы в использовании золотого сечения в своих работах, несколько простых советов заключаются в том, чтобы использовать шрифты, такие как шрифт заголовка и основной текст, чтобы они соответствовали золотому сечению. После того, как вы использовали золотое сечение в своей работе, вы сможете лучше определить эстетическую ценность золотого сечения. Золотое сечение в истории:Ранее мы обсуждали связь последовательности Фибоначчи и золотого сечения. Мы можем найти последовательность Фибоначчи в работах индийских математиков еще во втором или третьем веке до нашей эры. Позже его подхватили арабские математики, такие как Абу Камиль. От арабов оно было передано Леонардо Фибоначчи, чья знаменитая книга Liber abaci представила его западному миру. Мы уже упоминали некоторые древние сооружения, такие как пирамиды Гизы и Парфенон, в конструкции которых, как полагают, использовалось золотое сечение. Мы также находим упоминания о золотом сечении в трудах Платона. «Элементы» — древняя и известная книга по геометрии греческого математика Евклида. Мы находим некоторые из первых упоминаний о золотом сечении как о «крайнем и среднем соотношении» в «Элементах». Золотое сечение приобрело большую популярность в эпоху Возрождения. Лука Пачоли, 1509 год., опубликовал книгу о золотом сечении под названием «Божественная пропорция». Леонардо да Винчи сделал иллюстрации к этой книге. Художники эпохи Возрождения использовали концепцию золотого сечения в своих работах из-за ее эстетической привлекательности. Известный астроном Иоганн Кеплер также обсуждает в своих трудах золотое сечение, и мы также описали треугольник Кеплера выше. Считается, что термин «золотое сечение» был введен Мартином Омом в 1815 году в его книге «Чистая элементарная математика». Греческая буква фи (то есть $\Phi$), которую мы также использовали в этой статье для обозначения золотого сечения, впервые была использована в 1914 году американским математиком Марком Барром. Обратите внимание, что греческий $\Phi$ эквивалентен алфавиту «F», первой букве Фибоначчи. Совсем недавно Ле Корбюзье, ведущий архитектор секретариата ООН, создал систему проектирования, основанную на золотом сечении здания секретариата ООН. |