Производная по направлению, градиент функции: объяснение, примеры

• Понятие производной по направлению
• Примеры нахождения производной по направлению
• Градиент функции

Понятие производной по направлению рассматривается для функций двух и трёх переменных.
Чтобы понять смысл производной по направлению, нужно сравнить производные по определению

1) функции одной переменной;

2) функции трёх переменных в нашем случае.

Рассматривая функцию одной переменной, мы выяснили, что на оси Oy
отображается приращение функции f(x), соответствующее приращению
аргумента x. Если мы имеем дело с функцией трёх переменных, то приращения
аргументов x, y, z
отображаются на осях Оx, Оy, Оz.
Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?

И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой
прямой, направление которой определяется вектором, произвольно заданным в задаче.

Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы,
а упомянутая прямая, на которой отображается приращение функции, — это ещё одно измерение и для его акцентирования
назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт
чаще начинается не с единицы, а с нуля).

Для того, чтобы перейти к строгому математическому определению производной по направлению,
нужно рассмотреть:

1) функцию u = f(M),
определённую в окрестности точки M с координатами
x, y, z;

2) произвольный вектор l с направляющими косинусами
cosα, cosβ, cosγ.

Через точку M проводим прямую, одно из двух возможных
направлений которых совпадает с направлением вектора l. На получившейся
прямой отметим точку M1, координаты которой
образуют суммы координат точки M и приращений соответствующих
аргументов функции трёх переменных:

Величину отрезка MM1
можно обозначить .

Функция u = f(M) при этом
получит приращение

.

Определение производной по направлению. Предел отношения
при ,
если он существует, называется производной функции u = f(M)
по направлению вектора l и обозначается
, то есть

.

Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:

.

Смысл этой формулы: производная по направлению является линейной комбинацией
частных производных, причём
направляющие косинусы показывают вклад в производную по направлению
соответствующей частной производной.

Пример 1. Найти производную функции
в точке M0(1; 2; 3) по направлению вектора
.

Решение. Найдём частные производные функции в точке M0:

Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:

Следовательно,

Теперь можем найти производную по направлению данной функции по её формуле:

Нет времени вникать в решение? Можно заказать работу!

А сейчас — домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько
иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.

Пример 2. Найти производную функции
в точке M0(1; 2) по направлению вектора
, где M1 —
точка с координатами (3; 0).

Посмотреть правильное решение и ответ.

Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере —
в виде разложения по ортам координатных осей, но эта хорошо знакомая тема из самого начала векторной алгебры.

Пример 3. Найти производную функции
в точке M0(1; 1; 1) по направлению вектора
.

Решение. Найдём направляющие косинусы вектора

Найдём частные производные функции в точке M0:

Следовательно, можем найти производную по направлению данной функции по её формуле:

.

Градиент функции нескольких переменных в точке M0
характеризует направление максимального роста этой функции в точке M0 и
величину этого максимального роста.

Как найти градиент?

Нужно определить вектор, проекциями которого на оси координат
являются значения частных
производных ,
,
этой функции в соответствующей точке:

.

То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый
орт умножается соответствующая его оси частная производная.

Для градиента функции двух переменных формула короче:

.

Пример 4. Найти градиент функции
в точке
M0(2; 4;).

Решение. Найдём частные производные функции в точке M0:

Следовательно, можем записать искомый градиент данной функции:

.

К началу страницы

Пройти тест по теме Функции нескольких переменных

Поделиться с друзьями

Производные

• Что такое производная
• Найти производную: алгоритм и примеры решений
• Производные произведения и частного функций
• Производная суммы дробей со степенями и корнями
• Производные простых тригонометрических функций
• Производная сложной функции
• Производная логарифмической функции
• Уравнение касательной и уравнение нормали к графику функции
• Дифференциал функции
• Дифференциал сложной функции, инвариантность формы дифференциала
• Правило Лопиталя

Функции нескольких переменных

• Функция двух и более переменных. Её область определения
• Поверхности второго порядка
• Частные производные
• Касательная плоскость и нормаль к поверхности
• Производная по направлению, градиент функции
• Экстремумы функции двух переменных
• Условные экстремумы и функция Лагранжа

градиент, дивергенция и ротор MathCAD 12 руководство

• Дифференцирование
• 3. 1. Аналитическое дифференцирование
  • 3.1.1. Аналитическое дифференцирование функции
  • 3.1.2. Вычисление производной функции в точке
  • 3.1.3. Определение функций пользователя через оператор дифференцирования
  • 3.1.4. Дифференцирование при помощи меню

• 3.2. Численное дифференцирование
  • 3.2.1. Дифференцирование в точке
  • 3.2.2. Об алгоритме дифференцирования

• 3.3. Производные высших порядков
• 3.4. Частные производные
  • 3.4.1. Частные производные
  • 3.4.2. Примеры: градиент, дивергенция и ротор
  • 3.4.3. Пример: якобиан

• 3.5. Разложение функции в ряд Тейлора
  • 3.5.1. Разложение в ряд при помощи меню
  • 3.5.2. Оператор разложения в ряд

Завершим разговор о частных производных несколькими примерами векторного анализа, которые нередко встречаются в вычислительной практике. Программная реализация первого из них, посвященная вычислению градиента функции двух переменных, приведена в листинге 3.14. В качестве примера взята функция f(x,y), определяемая в первой строке листинга, график которой показан на рис. 3.9, в виде линий уровня. Как известно, градиент функции f(x,y) является векторной функцией тех же аргументов, что и
f (х,у), определенной через ее частные производные, согласно второй строке листинга 3.14. В его третьей строке производится аналитическое вычисление градиента, а в оставшейся части листинга задаются ранжированные переменные и матрицы, необходимые для подготовки графика линий уровня самой функции и графика векторного поля ее градиента (рис. 3.10).

Листинг 3.14. Вычисление градиента функции двух переменных

Рис. 3.9. Модельная функция двух переменных (продолжение листинга 3.14)

Рис. 3.10. Векторное поле градиента функции двух переменных (продолжение листинга 3.14)

Как можно убедиться, сравнив графики на рис. 3.9 и 3.10, математический смысл градиента состоит в задании в каждой точке (х,у) направления на
плоскости, в котором функция f (х,у) растет наиболее быстро. Абсолютное значение градиента (т. е. длина вектора в каждой точке) определяет локальную скорость изменения
f (x,y). Из сопоставления графи ков ясно, что в центре показанной на них области
(х,у) сама функция f (х,у) меняется медленно (соответственно, значения ее градиента являются малыми), а в углах — быстро (там значения градиента максимальны).

Очень важно заметить, что градиент является не скалярной, а векторной функцией переменных х,у, поскольку фактически представляет собой комбинацию двух функций, задающих соответствующие проекции (горизонтальную и вертикальную) вектора в каждой точке. До сих пор в данной главе мы рассматривали дифференцирование скалярных функций, однако в математике часто приходится иметь дело и с вычислением производных векторных функций. Рассмотрим эти действия на примере операции поиска дивергенции (листинг 3. 15 и рис. 3.11), применимой к векторному полю, т. е. векторной функции, зависящей от пространственных координат (на плоскости, как в нашем примере, или в трехмерном пространстве).

Листинг 3.15. Вычисление дивергенции векторной функции

Если, как принято в математике, обозначить оператор взятия градиента символом V, то дивергенцию вектор-функции можно формально определить как скалярное произведение
Vf, а еще одну распространенную операцию векторного анализа — ротор (или, по-другому, вихрь или завихренность) — как векторное произведение Vxf. Рис. 3.11 иллюстрирует пример векторной функции f (х,у) (определяемой в первой строке листинга) и вычисление ее дивергенции (которое производится аналитически в третьей строке). Обратите внимание, что в качестве исходной вектор-функции взят результат предыдущих расчетов, показанный (в форме векторного поля) на рис. 3.10. Строки кода в верхней части рис. 3.11 нужны для подготовки графика вычисленной дивергенции (в виде трехмерной поверхности и линий уровня, соответственно сверху и снизу).

Точно такую же структуру имеют расчеты ротора той же векторной функции f (х,у) в листинге 3.16, причем определение операции взятия ротора приводится в его второй строке (как и в случае дивергенции для листинга 3.15).

Читателю, знакомому с векторным анализом, предлагается догадаться самому, почему в рассматриваемом примере (листинги 3.14—3.16) ротор получается тождественно равным нулю (последняя строка листинга 3.16).

Рис. 3.11. График дивергенции векторной функции (продолжение листинга 3.15)

Листинг 3.16. Вычисление ротора векторной функции

В заключение разговора о векторном анализе функций подчеркнем, что примеры в листингах 3.14—3.16 относились к функциям двух переменных,
т. е. описывали двумерный случай. Еще два листинга — 3.17 и 3.18 — показывают, как действуют перечисленные операции векторного анализа в трехмерном (пространственном) случае.

ПРИМЕЧАНИЕ

В электронной книге Resource Center (Центр ресурсов), поставляемой вместе с Mathcad, вы найдете дополнительные примеры вычисления градиента, дивергенции и ротора, относящихся к трехмерному случаю.

Листинг 3.17. Градиент функции трех переменных

Листинг 3.18. Дивергенция и ротор в трехмерном пространстве

Нравится

Твитнуть

2\\
\pdiff{f}{x}(3,2) & = 12 &
\pdiff{f}{y}(3,2) & = 9
\конец{выравнивание*}
Следовательно, градиент равен
\начать{выравнивать*}
\nabla f (3,2) = 12 \vc{i} + 9 \vc{j} = (12,9).
\конец{выравнивание*}

(b) Пусть $\vc{u}=u_1\vc{i} + u_2 \vc{j}$ — единичный вектор.
производная по направлению в точке (3,2) в направлении $\vc{u}$ равна
\начать{выравнивать}
D_{\vc{u}}f(3,2) &= \nabla f(3,2) \cdot \vc{u}\notag\\
&= (12 \vc{i} + 9 \vc{j}) \cdot (u_1\vc{i} + u_2 \vc{j})\notag\\
&= 12 и_1 + 9 и_2.
\label{Дублировать}
\end{выравнивание}
92}} = \frac{(1,2)}{\sqrt{5}} =
(1/\sqrt{5},2/\sqrt{5}).
\конец{выравнивание*}
Подставив это выражение для $\vc{u} = (u_1, u_2)$ в
уравнение \eqref{Dub}
для производной по направлению, и мы находим, что
производная по направлению в точке $(3,2)$ в направлении
$(1,2)$ это
\начать{выравнивать*}
D_{\vc{u}}f(3,2) &= 12 u_1 + 9 u_2\\
&= \frac{12}{\sqrt{5}} + \frac{18}{\sqrt{5}}
= \frac{30}{\sqrt{5}}.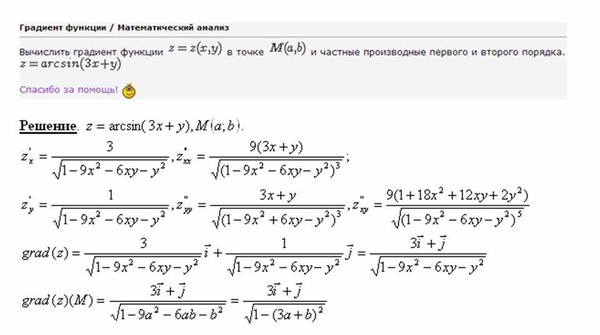
\конец{выравнивание*}

Пример 2

Для $f$ Примера 1,
найти производную по направлению от $f$ в точке
точку (3,2) в направлении $(2,1)$.

Решение : Единичный вектор в направлении $(2,1)$ равен
\начать{выравнивать*}
\vc{u} = \frac{(2,1)}{\sqrt{5}} = (2/\sqrt{5},1/\sqrt{5}).
\конец{выравнивание*}
Поскольку мы все еще находимся в точке (3,2),
уравнение \eqref{Dub}
все еще
действительный. Мы подключаем наш новый $\vc{u}$, чтобы получить
\начать{выравнивать*}
D_{\vc{u}}f(3,2) &= 12 u_1 + 9 u_2\\
&= \frac{24}{\sqrt{5}} + \frac{9}{\sqrt{5}}
= \frac{33}{\sqrt{5}}
\конец{выравнивание*}

Пример 3

Для $f$ Примера 1 в точке (3,2), (a) в каком направлении
производная по направлению максимальна, (b) какова направленность
производная в этом направлении? 92} = 15$. Следовательно
производная по направлению в точке (3,2) в направлении (12,9)
равно 15.

Мы могли бы перепроверить, вычислив результат, используя
уравнение \eqref{Dub}
и единичный вектор $\vc{u} = (4/5,3/5)$. {0 }\больше) = (92} = \sqrt{26}$,
\начать{выравнивать*}
\vc{u}=\frac{\vc{v}}{\sqrt{26}} = \left(\frac{3}{\sqrt{26}}, \frac{-1}{\sqrt{26 }}, \frac{4}{\sqrt{26}}\right)
\конец{выравнивание*}
а также
\начать{выравнивать*}
D_{\vc{u}}f(1,3,-2) &= \nabla f(1,3,-2) \cdot \vc{u}\\
&=(9,1,-12) \cdot \left(\frac{3}{\sqrt{26}}, \frac{-1}{\sqrt{26}}, \frac{4}{\sqrt {26}}\справа)\\
&= \frac{9\cdot 3- 1-12\cdot 4}{\sqrt{26}}=\frac{-22}{\sqrt{26}}.
\конец{выравнивание*}

Градиент: определение и примеры — Статистика Как сделать

Определения исчисления >

Термин градиент имеет как минимум два значения в исчислении. Обычно это относится к:

• Наклон функции. Например, в учебнике по математике AS Use of Maths [1] 2004 г. говорится, что «…прямые линии имеют фиксированные градиенты (или наклоны)» (стр. 16). Многие старые учебники (например, , этот из 1914 года) также склонны использовать слово «градиент» для обозначения уклона.
• Особый тип производной с несколькими переменными.  

Эта статья в основном посвящена градиенту применительно к частным производным. Если вы хотите познакомиться со склонами, см.: что такое уклон? Вы также можете найти несколько простых примеров нахождения градиента (наклона) ниже.

Градиент против производной и вектора градиента

Градиент может относиться к производной функции. Хотя производная функции одной переменной может можно назвать градиентом, этот термин чаще используется для сложных, многовариантных ситуаций, когда у вас есть несколько входов и один выход. В этих случаях вектор градиента хранит всю информацию о частных производных для каждой переменной.

Для функции f градиент обычно обозначается град f или Δf.

Нахождение градиента для функций с несколькими переменными

Чтобы найти градиент для функций с несколькими переменными, найдите частные производные для каждой переменной.

Пример вопроса: Найдите Δf для функции
f(x,y) = x ² + y ³ .

Шаг 1: Найдите частную производную f по x . Для этого оставьте y постоянным, и вам останется только найти производную от x ² , которая равна 2x (здесь я использовал правило степени). Это дает:
2x + y ³ = 2xy ³ .

Шаг 2: Найдите частную производную f по y . На этот раз оставьте x постоянным; найти только производную от y ³ , что составляет 3 года ² . Это дает:
x ² + 2y ² = 3x ² y ²

Шаг 3: Перепишите ответы из предыдущих шагов в формате Δf, который аналогичен записи координат (x, y):

Grad f (x,y) = (2xy ³ , 3x ² y ² )

Это градиент для указанной функции, но иногда вы можете захотеть найти его с помощью определенных входных данных, как град ф (1, 2).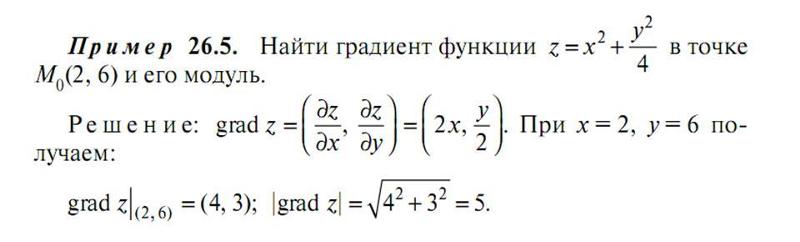 Для этого достаточно заменить x, y в частных производных на (1, 2).

Примечание : Неважно, сколько переменных; процедура такая же. Итак, чтобы найти градус w = g(x,y,z), возьмите частную производную от x, y и z соответственно. Поскольку g имеет три переменные, Δg имеет три члена.

Часто вам дают график с прямой линией и просят найти градиент линии. Вы можете использовать следующую формулу:

G = изменение координаты y / изменение координаты x
Иногда это записывается как
G = Δy / Δx

Давайте рассмотрим пример прямолинейного графика с двумя заданными точками (A и B).

Заполнение координат точек A и B:

G = (3-0)/(0-6) = 3/-6 = -1/2

В этом примере градиент — ½. Вы также можете использовать градиент, чтобы найти уравнение приведенной выше линии (уравнение для линейной функции y = mx + b). Линия пересекает ось y в точке B, когда y = 3. Таким образом, уравнение будет иметь вид y = -½ + 3.

Градиент кривой

Кроме прямой линии вас могут попросить найти градиент кривой. Чтобы вычислить его, вы можете провести касательную к кривой — линию, которая касается кривой в одной точке. Затем вы вычисляете градиент этой единственной линии — касательной.

Пример :

Найдите градиент кривой в точке (2, 7)

Как вы можете видеть на графике выше, касательная касается кривой вокруг точки (1, 3). Вы можете использовать ту же формулу, что и формула для прямой линии: (изменение y)/(изменение x)

Подставляя числа в формулу:

(7-3)/2-1) = 4/1

Градиент кривой в точке (2, 7) равен 4.

Ссылки

[1 ] Хейтон, Дж. Хаворт, А. (2004). AS Использование математики. Нельсон Торнс.
Годфри, К. и Синнонс, А. (1914). Первые шаги в расчетах. Издательство Кембриджского университета.
Хейтон, Дж. и Хаворт, А. (2004). AS — Использование математики — Исчисление. Нельсон Торнс.
Градиенты и производная по направлению.