Содержание
Градиент
Градиент
Производная
по направлению. Градиент
Пусть в некоторой области
задана функция
и точка .
Проведем из точки
вектор ,
направляющие косинусы которого .
На векторе ,
на расстоянии
от его начала рассмотрим точку ,
т.е. .
Будем предполагать, что функция
и ее частные производные первого порядка непрерывны в области .
Предел отношения
при называется
производной от функции
в точке по
направлению вектора
и обозначается ,
т.е.
.
Для нахождения производной от функции
в заданной точке по
направлению вектора
используют формулу: ,
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
.
Пусть в каждой точке некоторой
области
задана функция .
Вектор, проекциями которого на оси координат являются значения частных производных
этой функции в соответствующей точке, называется градиентом функции
и обозначается
или
(читается «набла у»): .
При этом говорят, что в области
определено векторное поле градиентов.
Для нахождения градиента функции
в заданной точке
используют формулу:
.
Свойства
градиента
1. Производная
в данной точке по направлению вектора
имеет наибольшее значение, если направление вектора
совпадает с направлением градиента. Это наибольшее значение производной равно
.
2. Производная
по направлению вектора, перпендикулярного к вектору ,
равна нулю.
Примеры
решения задач
Пример 1.
Найти производную от функции
в точке
по направлению вектора .
Решение.
Для решения задачи воспользуемся
формулой для нахождения производной от функции
в заданной точке
по направлению вектора :
,
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
.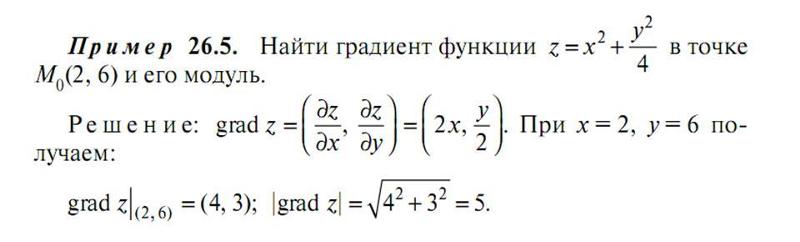
По условию задачи вектор
имеет координаты .
Тогда его длина равна:
.
Следовательно, для направляющих косинусов вектора получим следующие значения:
.
Далее для решения задачи необходимо найти все частные производные первого порядка
от функции :
Вычислим значения этих частных производных первого порядка в точке :
В заключении подставим полученные значения для направляющих косинусов вектора
и значения частных производных первого порядка от функции в
точке
в формулу для нахождения производной по направлению в заданной точке:
Ответ: производная от функции
в точке
по направлению вектора
равна .
Пример 2.
Найти градиент функции
в точке .
Решение.
Поскольку градиентом функции
называется вектор, проекциями которого на оси координат являются значения частных
производных этой функции в соответствующей точке, то для решения задачи сначала
найдем все частные производные первого порядка от заданной функции:
Далее вычислим значения этих частных производных первого порядка в точке :
Подставим полученные значения в формулу градиента функции
в заданной точке :
.
Ответ: градиент функции
в точке
равен .
Пример 3.
Найти производную функции
в точке
по направлению градиента функции
в той же точке.
Решение.
Для нахождения производной
от функции
в заданной точке
по направлению вектора
используют формулу:
,
где
– направляющие косинусы вектора ,
которые вычисляются по формулам:
.
В данном случае вектор совпадает
с градиентом функции
в точке :
.
Следовательно, для решения задачи необходимо найти значения всех частных производных
первого порядка от функции
в точке ,
а также координаты и длину градиента функции
в той же точке.
Вычислим значения частных производных первого порядка от функции
в точке :
Для нахождения координат вектора ,
равного градиенту функции
в заданной точке ,
вычислим значения частных производных первого порядка от функции
в этой точке:
Длина вектора равна: .
Найдем направляющие косинусы вектор по формулам:
.
Подставим полученные значения в формулу для нахождения производной от функции
в заданной точке
по направлению вектора :
Ответ: производная функции
в точке по
направлению градиента функции
в той же точке равна 1.
Задания
для самостоятельной работы
1.
Найти производную функции
в точке
по направлению вектора .
Ответ: .
2. Найти производную функции
в точке
по направлению вектора .
Ответ: .
3. Найти производную функции
в точке
по направлению вектора .
Ответ: .
4. Найти градиент функции
в точке .
Ответ: .
5. Найти градиент функции
в точке .
Ответ: .
6. Найти градиент функции
в точке .
Ответ:
.
Производная по направлению, градиент функции: объяснение, примеры
- Понятие производной по направлению
- Примеры нахождения производной по направлению
- Градиент функции
Понятие производной по направлению рассматривается для функций двух и трёх переменных.
Чтобы понять смысл производной по направлению, нужно сравнить производные по определению
1) функции одной переменной;
2) функции трёх переменных в нашем случае.
Рассматривая функцию одной переменной, мы выяснили, что на оси Oy
отображается приращение функции f(x), соответствующее приращению
аргумента x. Если мы имеем дело с функцией трёх переменных, то приращения
аргументов x, y, z
отображаются на осях Оx, Оy, Оz.
Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?
И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой
прямой, направление которой определяется вектором, произвольно заданным в задаче.
Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы,
а упомянутая прямая, на которой отображается приращение функции, — это ещё одно измерение и для его акцентирования
назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт
чаще начинается не с единицы, а с нуля).
Для того, чтобы перейти к строгому математическому определению производной по направлению,
нужно рассмотреть:
1) функцию u = f(M),
определённую в окрестности точки M с координатами
x, y, z;
2) произвольный вектор l с направляющими косинусами
cosα, cosβ, cosγ.
Через точку M проводим прямую, одно из двух возможных
направлений которых совпадает с направлением вектора l. На получившейся
прямой отметим точку M1, координаты которой
образуют суммы координат точки M и приращений соответствующих
аргументов функции трёх переменных:
Величину отрезка MM1
можно обозначить .
Функция u = f(M) при этом
получит приращение
.
Определение производной по направлению. Предел отношения
при ,
если он существует, называется производной функции u = f(M)
по направлению вектора l и обозначается
, то есть
.
Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:
.
Смысл этой формулы: производная по направлению является линейной комбинацией
частных производных, причём
направляющие косинусы показывают вклад в производную по направлению
соответствующей частной производной.
Пример 1. Найти производную функции
в точке M0(1; 2; 3) по направлению вектора
.
Решение. Найдём частные производные функции в точке M0:
Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:
Следовательно,
Теперь можем найти производную по направлению данной функции по её формуле:
Нет времени вникать в решение? Можно заказать работу!
А сейчас — домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько
иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.
Пример 2. Найти производную функции
в точке M0(1; 2) по направлению вектора
, где M1 —
точка с координатами (3; 0).
Посмотреть правильное решение и ответ.
Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере —
в виде разложения по ортам координатных осей, но эта хорошо знакомая тема из самого начала векторной алгебры.
Пример 3. Найти производную функции
в точке M0(1; 1; 1) по направлению вектора
.
Решение. Найдём направляющие косинусы вектора
Найдём частные производные функции в точке M0:
Следовательно, можем найти производную по направлению данной функции по её формуле:
.
Градиент функции нескольких переменных в точке M0
характеризует направление максимального роста этой функции в точке M0 и
величину этого максимального роста.
Как найти градиент?
Нужно определить вектор, проекциями которого на оси координат
являются значения частных
производных ,
,
этой функции в соответствующей точке:
.
То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый
орт умножается соответствующая его оси частная производная.
Для градиента функции двух переменных формула короче:
.
Пример 4. Найти градиент функции
в точке
M0(2; 4;).
Решение. Найдём частные производные функции в точке M0:
Следовательно, можем записать искомый градиент данной функции:
.
К началу страницы
Пройти тест по теме Функции нескольких переменных
Поделиться с друзьями
Производные
- Что такое производная
- Найти производную: алгоритм и примеры решений
- Производные произведения и частного функций
- Производная суммы дробей со степенями и корнями
- Производные простых тригонометрических функций
- Производная сложной функции
- Производная логарифмической функции
- Уравнение касательной и уравнение нормали к графику функции
- Дифференциал функции
- Дифференциал сложной функции, инвариантность формы дифференциала
- Правило Лопиталя
Функции нескольких переменных
- Функция двух и более переменных.
 Её область определения
Её область определения - Поверхности второго порядка
- Частные производные
- Касательная плоскость и нормаль к поверхности
- Производная по направлению, градиент функции
- Экстремумы функции двух переменных
- Условные экстремумы и функция Лагранжа
2\\
\pdiff{f}{x}(3,2) & = 12 &
\pdiff{f}{y}(3,2) & = 9
\конец{выравнивание*}
Следовательно, градиент равен
\начать{выравнивать*}
\nabla f (3,2) = 12 \vc{i} + 9 \vc{j} = (12,9).
\конец{выравнивание*}
(b) Пусть $\vc{u}=u_1\vc{i} + u_2 \vc{j}$ — единичный вектор.
производная по направлению в точке (3,2) в направлении $\vc{u}$ равна
\начать{выравнивать}
D_{\vc{u}}f(3,2) &= \nabla f(3,2) \cdot \vc{u}\notag\\
&= (12 \vc{i} + 9 \vc{j}) \cdot (u_1\vc{i} + u_2 \vc{j})\notag\\
&= 12 и_1 + 9 и_2.
\label{Дублировать}
\end{выравнивание}
92}} = \frac{(1,2)}{\sqrt{5}} =
(1/\sqrt{5},2/\sqrt{5}).
\конец{выравнивание*}
Подставив это выражение для $\vc{u} = (u_1, u_2)$ в
уравнение \eqref{Dub}
для производной по направлению, и мы находим, что
производная по направлению в точке $(3,2)$ в направлении
$(1,2)$ это
\начать{выравнивать*}
D_{\vc{u}}f(3,2) &= 12 u_1 + 9 u_2\\
&= \frac{12}{\sqrt{5}} + \frac{18}{\sqrt{5}}
= \frac{30}{\sqrt{5}}.
\конец{выравнивание*}
Пример 2
Для $f$ Примера 1,
найти производную по направлению от $f$ в точке
точку (3,2) в направлении $(2,1)$.
Решение : Единичный вектор в направлении $(2,1)$ равен
\начать{выравнивать*}
\vc{u} = \frac{(2,1)}{\sqrt{5}} = (2/\sqrt{5},1/\sqrt{5}).
\конец{выравнивание*}
Поскольку мы все еще находимся в точке (3,2),
уравнение \eqref{Dub}
все еще
действительный. Мы подключаем наш новый $\vc{u}$, чтобы получить
\начать{выравнивать*}
D_{\vc{u}}f(3,2) &= 12 u_1 + 9 u_2\\
&= \frac{24}{\sqrt{5}} + \frac{9}{\sqrt{5}}
= \frac{33}{\sqrt{5}}
\конец{выравнивание*}
Пример 3
Для $f$ Примера 1 в точке (3,2), (a) в каком направлении
производная по направлению максимальна, (b) какова направленность
производная в этом направлении? 92} = 15$. Следовательно
производная по направлению в точке (3,2) в направлении (12,9)
равно 15.
Мы могли бы перепроверить, вычислив результат, используя
уравнение \eqref{Dub}
и единичный вектор $\vc{u} = (4/5,3/5)$. {0 }\больше) = (92} = \sqrt{26}$,
{0 }\больше) = (92} = \sqrt{26}$,
\начать{выравнивать*}
\vc{u}=\frac{\vc{v}}{\sqrt{26}} = \left(\frac{3}{\sqrt{26}}, \frac{-1}{\sqrt{26 }}, \frac{4}{\sqrt{26}}\right)
\конец{выравнивание*}
и
\начать{выравнивать*}
D_{\vc{u}}f(1,3,-2) &= \nabla f(1,3,-2) \cdot \vc{u}\\
&=(9,1,-12) \cdot \left(\frac{3}{\sqrt{26}}, \frac{-1}{\sqrt{26}}, \frac{4}{\sqrt {26}}\справа)\\
&= \frac{9\cdot 3- 1-12\cdot 4}{\sqrt{26}}=\frac{-22}{\sqrt{26}}.
\конец{выравнивание*}
Определение градиента — объяснение и примеры
Следующие свойства градиента помогают понять ориентацию линии.
Для линии, проведенной в n-мерном пространстве, градиент линии относительно определенного измерения называется ее производной по направлению.
Понятие частной производной помогает найти производную по направлению. И это представлено как \(\frac{\delta y}{\delta x} \)
Здесь частная производная по x дает производную по направлению в направлении оси x. В этом выражении z рассматривается как константа.
\[\begin{align} \frac{\delta y}{\delta x} &= \frac{\delta}{\delta x}(5x + 4z + 3xz + 11) \\ \frac{\delta y}{\delta x} &= \frac{\delta}{\delta x}(5x) + \frac{\delta}{\delta x}(4z) + \frac{\delta}{\delta x} (3xz)
+ \frac{\delta}{\delta x}(11) \\\frac{\delta y}{\delta x} &= 5(1) + 0 + 3(1)z + 0 \\\frac{ \delta y}{\delta x} &=5 + 3z\end{align} \]
\(\следовательно \) 5 + 3z — это производная по направлению уравнения прямой относительно оси x.
Think Tank
Уравнение y = mx + c называется формой пересечения наклона. Здесь «m» — это наклон, а «c» — точка пересечения линии по оси Y.
Найдите наклон и точку пересечения по оси Y линии, имеющей уравнение 4x -90 \\ m &=\sqrt3 \end{align} \]
| \(\следовательно \) Градиент лестницы равен \(\sqrt 3 \) |
| Пример 2 |
Альберт отмечает на миллиметровке две точки (4, 3) и (6, 7) и проводит линию, проходящую через эти точки. 2 -5x + 8 \) в точке (1, 6). Найдите градиент этой линии. 92 + 4(1) – 5 \\ m &= 3 + 4 – 5 \\ m &= 7 – 5 \\ m &= 2 \end{align} \]
2 -5x + 8 \) в точке (1, 6). Найдите градиент этой линии. 92 + 4(1) – 5 \\ m &= 3 + 4 – 5 \\ m &= 7 – 5 \\ m &= 2 \end{align} \]
| \(\поэтому \) Градиент касательной равен 2 |
| Пример 4 |
Шерил рисует две параллельные линии, и уравнение одной линии 2x – y + 5 = 0. Найдите градиент другой линии.
Решение
Данное уравнение прямой имеет вид 2x – y = 5
Кроме того, градиент двух параллельных линий равен.
Найдем градиент этой линии.
\[\begin{align} 2x -y + 5 &= 0 \\ -y &= -2x -5 \\ y &= 2x + 5 \end{align} \]
Сравнивая это с наклоном- y = mx + c получаем m = 2
Градиент этой линии равен 2
Следовательно, искомый градиент параллельной линии равен m = 2
| \(\следовательно \) уклон параллельной линии равен 2 |
| Пример 5 |
Учитель просит Сэма нарисовать набор перпендикулярных линий и записать наклон одной линии как 2. Помогите Сэму найти наклон другой линии.
Помогите Сэму найти наклон другой линии.
Решение
Наклон данной линии равен \(m_1 \) = 2
Произведение наклонов двух перпендикулярных линий равно -1
\[\begin{align} m_1.m_2 &= -1 \\ 2 \times m_2 &= -1 \\ m_2 &= \frac{-1}{2}\end{align} \]
| \(\следовательно \) Наклон линии равен \(\frac{-1}{2}\) |
Интерактивные вопросы по градиенту
Вот несколько упражнений для практики. Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
9007 суммируем0086
Мини-урок был посвящен увлекательной концепции градиента. Математическое путешествие по градиенту началось с основ градиента и продолжилось творческим созданием новой концепции, включающей формулы и уравнения. Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда.
Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда.
О Cuemath
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, мы в Cuemath верим в логическое мышление и разумный подход к обучению. , Что такое определение градиента?
Градиент — это наклон линии. Он измеряется углом, который линия образует с опорной осью X. Кроме того, две точки на линии или уравнение линии помогают найти градиент.
\[m = tan\theta = \frac{y_2 — y_1}{x_2 — x_1} = \frac{d}{dx}.f(x) \]
2. Что такое градиент матрицы?
Для матрицы, содержащей в качестве элементов различные функции (уравнения), производная этих элементов, представленная в матричной форме, называется градиентом матрицы.

 Её область определения
Её область определения