Рецепты частотного разложения
Метод частотного разложения, на мой взгляд – это лучшая на сегодняшний день технология, позволяющая отдельно работать с детализацией и цветом. Для тех, кому интересны теоретические основы этого метода, рекомендую почитать соответствующие материалы в ЖЖ Андрея Журавлева, так как не вижу смысла дублировать то, что уже было сделано до меня, причем, максимально подробно, с описанием математики.
Мы же с вами коснемся чисто практических аспектов и нюансов применения данного метода, рассмотрим как достоинства, так и недостатки, а точнее, ограничения различных способов реализации метода частотного разложения.
Если вы уже сталкивались с этим методом, то знаете, что существует несколько способов его реализации.
Разложение на две частоты с помощью фильтров Размытие по Гауссу (Gaussian Blur) и Цветовой контраст (High Pass).
Именно этот метод получил поначалу самое широкое распространение в сети. Он прост в реализации, но имеет некоторые ограничения в применении. Для начала кратко рассмотрим сам метод.
Для начала кратко рассмотрим сам метод.
Для того, чтобы разложить изображение на две частоты, нужно выполнить следующие операции:
1. Создаем копию фонового слоя или объединяем видимые слои на отдельный слой.
2. Называем ее как-то осмысленно, исходя из того, что этот слой будет являться основой для дальнейших действий. Например, Base или Основа.
3. Делаем две копии слоя Base. Первую называем Low или Низкая частота, вторую, соответственно, High или Высокая частота.
4. Дальнейшие действия зависят от того, на какую составляющую мы будем ориентироваться. Если нам важно вынести на слой High всю хорошую текстуру, оставив более крупные дефекты на слое Low, то поступаем следующим образом:
5. К слою High применяем фильтр Цветовой контраст (High Pass) с таким радиусом, чтобы видеть только ту текстуру кожи, которая нам нужна. Радиус не должен быть слишком малым, иначе часть хорошей текстуры уйдет на слой с низкой частотой, то есть Low. Также он не должен быть и слишком большим, чтобы не выносить на слой с высокой частотой те самые, более крупные дефекты в виде локальных объемов, от которых нам необходимо избавляться.
Радиус не должен быть слишком малым, иначе часть хорошей текстуры уйдет на слой с низкой частотой, то есть Low. Также он не должен быть и слишком большим, чтобы не выносить на слой с высокой частотой те самые, более крупные дефекты в виде локальных объемов, от которых нам необходимо избавляться.
Неправильный выбор радиуса фильтра Цветовой контраст. Слишком большой радиус.
Неправильный выбор радиуса фильтра Цветовой контраст. Слишком маленький радиус.
Оптимальный радиус фильтра Цветовой контраст
6. Подобрав необходимый радиус фильтра Цветовой контраст (High Pass), например, 5 пикселей, запоминаем его и применяем. Очень желательно прописать радиус фильтра в названии слоя. Например, High 5. Дело в том, что если вас неожиданно отвлекут от работы, например, телефонным звонком, вы вполне можете забыть значение и тогда придется начинать все заново.
7. Применяем фильтр Размытие по Гауссу (Gaussian Blur) с таким же радиусом, то есть, в данном случае, 5 пикселей.
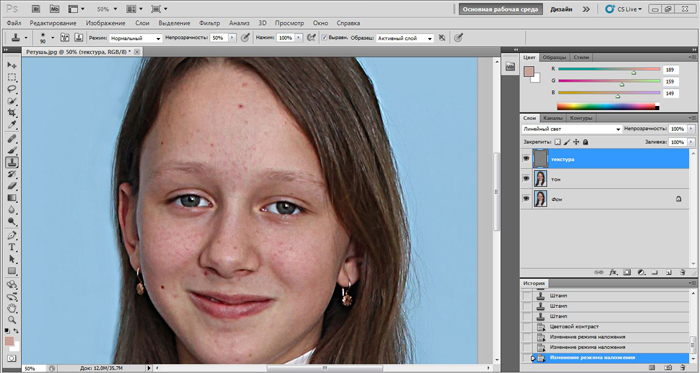
8. Меняем режим наложения слоя High на Линейный свет (Linear light)
9. Снижаем контраст слоя High в два раза. Для этого создаем корректирующий слой Яркость/Контрастность, включаем параметр Использовать прежние и ставим значение контраста на минус 50. Применяем через обтравочную маску к слою High.
10. Мы разложили изображение на две частоты. Теперь можно по отдельности работать с детализацией, цветом и объемом. Я не буду подробно останавливаться на процессе, так как подробнее вы можете узнать об этом, купив запись онлайн мастер-класса «Частотное разложение — просто как 2х2»
11. Если же нам важно наоборот, контролировать, какие дефекты останутся на низкой частоте, то есть, работа с низкой частотой в приоритете, то нужно сначала отключить видимость слоя High, затем подобрать нужный радиус Размытия по Гауссу для слоя Low, прописать это значение в названии слоя, а затем, включив видимость слоя High, применить фильтр Цветовой контраст с тем же радиусом, что и фильтр Размытие по Гауссу. Далее все аналогично.
Далее все аналогично.
12. После этого можно создать дополнительные слои для ретуши низкочастотной и высокочастотной составляющих.
Достоинства метода: простота в освоении даже для новичков, возможность временно усилить текстуру для ретуши путем простого отключения корректирующего слоя, снижающего контраст.
Недостатки и ограничения метода: недостаточная гибкость, по сравнению с разложением изображения на три пространственных частоты, опасность появления артефактов на контрастных границах при работе на слое с текстурой, некоторая математическая неточность, обусловленная особенностью математики фильтра Цветовой контраст (подробнее об этом можно почитать здесь). Впрочем, надо отметить, что в 99% случаев этой погрешностью можно пренебречь, так как вы сами при ретуши вносите гораздо более существенные «погрешности», несоизмеримо большие.
Разложение на две частоты с помощью операции вычитания.
Для реализации этого метода нужно выполнить следующее:
1. Сделайте копию фонового слоя или копию видимых слоев, аналогично предыдущему алгоритму.
Сделайте копию фонового слоя или копию видимых слоев, аналогично предыдущему алгоритму.
2. Точно также сделайте две копии, назвав одну Low, а другую High.
3. Отключите видимость слоя High.
4. Подберите радиус размытия для слоя Low, примените фильтр Размытие по Гауссу.
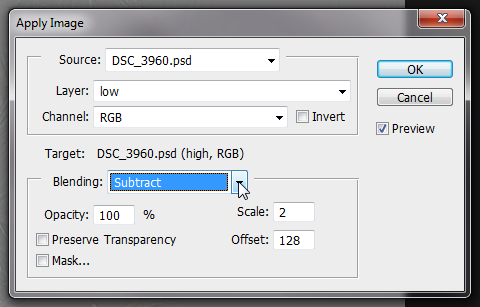
5. Перейдите на слой High. Если вы работаете с глубиной цвета 8 бит, то примените команду Внешний канал (Apply Image), установив следующие параметры – слой Low, канал RGB, режим наложения Вычитание, масштаб 2, сдвиг 128. Если вы работаете с глубиной цвета 16 бит, то примените команду Внешний канал, установив следующие параметры – слой Low, канал RGB, инвертировать, режим наложения Добавление, масштаб 2, сдвиг 0.
Параметры команды Внешний канал для режима 8 бит
Параметры команды Внешний канал для режима 16 бит
6. Измените режим наложения слоя High на Линейный свет (Linear light).
Достоинства метода: более аккуратная математика, отсутствие «проблемы High Pass», возможность применения любых фильтров размытия, а не только Размытия по Гауссу. Например, за счет применения фильтра Размытие по поверхности можно полностью решить проблему грязи на контрастных границах, легкость применения при построении «частотных эквалайзеров», то есть, многополосного разложения на пространственные частоты.
Недостатки метода: необходимость дополнительных операций для визуализации высокой частоты. Как выполнить такую визуализацию, я расскажу в конце статьи. Также к недостаткам (скорее к особенностям) метода можно отнести недостаточный контраст слоя High, что вызывает необходимость создания дополнительного корректирующего слоя, повышающего контраст, для облегчения ретуши высокочастотной составляющей. Точно также, метод имеет недостаточную гибкость, по сравнению с разложением на три пространственных частоты.
Точно также, метод имеет недостаточную гибкость, по сравнению с разложением на три пространственных частоты.
Разложение на три полосы частот.
Обеспечивает гораздо большую гибкость в работе, чем двухполосные методы. В частности, на низкой частоте можно полностью сосредоточиться на крупных участках, цвете, светотеневом рисунке, на высокую частоту вынести только необходимую текстуру, а все остальное оставить на промежуточной, средней частоте. В диапазон средних частот попадают такие дефекты как родинки, прыщи, пигментация кожи, веснушки, целлюлит, растяжки и т.д. Ретушируя среднюю полосу частот, мы избавляемся от этих дефектов. Иногда можно встретить рекомендации размывать среднюю полосу или просто вырубать ее черным цветом на маске. Я считаю такой подход несколько некорректным, так как именно ретушь средней полосы частот даст гораздо лучший результат.
Именно метод с разложением на три полосы частот я использую для ретуши фотографий, к которым предъявляются очень высокие требования по качеству постобработки. Подробный процесс ретуши со всеми объяснениями вы сможете найти в обучающем онлайн-курсе с домашними заданиями «Секреты профессиональной ретуши»
Подробный процесс ретуши со всеми объяснениями вы сможете найти в обучающем онлайн-курсе с домашними заданиями «Секреты профессиональной ретуши»
Как разложить изображение на три пространственных частоты:
1. Делаем базовый слой, как описано выше.
2. Создаем три копии слоя, называя их соответственно Low, Mid и High.
3. Подбираем радиус фильтра Цветовой контраст для слоя High. На этом слое будет только текстура кожи, без излишней информации о локальных объемах и дефектах. Радиус фильтра прописываем в названии слоя.
4. Подбираем радиус фильтра Размытие по Гауссу для слоя Low. Основным критерием здесь является размытие дефектов мелких и средних размеров. Должны остаться только дефекты относительно крупные, такие как следы крупных родимых или пигментных пятен, неровностей светотеневого рисунка. Однако, переусердствовать тоже не следует, иначе средняя частота получится слишком широкой. Как показала практика, оптимальное соотношение между высокой и низкой частотой в большинстве случаев лежит в пределах от 1:3 до 1:4, то есть, радиус размытия в 3-4 раза больше радиуса фильтра Цветовой контраст. Прописываем радиус фильтра в названии слоя.
Как показала практика, оптимальное соотношение между высокой и низкой частотой в большинстве случаев лежит в пределах от 1:3 до 1:4, то есть, радиус размытия в 3-4 раза больше радиуса фильтра Цветовой контраст. Прописываем радиус фильтра в названии слоя.
5. Все, что лежит между этими радиусами, будет вынесено в среднюю полосу частот. Для этого переходим на слой Mid и выполняем вычитание из него слоя Low. Делаем это с помощью команды Внешний канал, аналогично тому, как делали разложение на две частоты. Таким образом мы убиваем двух зайцев: получаем честный математический алгоритм, что критично для довольно больших радиусов, а также имеем возможность использовать на слое НЧ любые фильтры размытия, отличные от гауссова.
6. Размываем слой Mid по Гауссу с радиусом, который использован на слое High для фильтра Цветовой контраст.
7. Меняем режим наложения слоя Mid на Линейный свет.
Меняем режим наложения слоя Mid на Линейный свет.
8. Меняем режим наложения слоя High на Линейный свет. Уменьшаем контраст этого слоя в два раза, аналогично первому методу.
9. Теперь мы сможем работать раздельно с тремя пространственными частотами.
Достоинства метода: больше гибкости в работе, более качественный результат ретуши.
Недостатки метода: те же, что и у метода с разложением на две частоты, требуется больше времени для ретуши, так как приходится работать на трех слоях, вместо двух. Сложность в освоении метода, если нет необходимых базовых знаний Photoshop.
Полосовой фильтр.
Этот метод в зарубежных источниках имеет название Inverted High Pass, однако, по аналогии с электрическими фильтрами, здесь имеет место простое подавление некоторой полосы частот, то есть это аналог режекторного или полосового фильтра.
Полосовой фильтр хорошо использовать для быстрой ретуши, когда требуется с минимальными затратами времени и приемлемым для массовых работ качеством избавиться от дефектов в средней полосе частот.
Алгоритм действий:
1. Делаем копию фонового слоя, называя ее, например, Fast Retouch, то есть Быстрая Ретушь.
2. Размываем данный слой по Гауссу с таким радиусом, чтобы убрать ненужные локальные объемы.
3. Вычитаем из размытого слоя исходный, то есть, в данном случае процесс происходит наоборот, так как в предыдущих методах мы вычитали из исходного слоя как раз размытый. Делаем это с помощью команды Внешний канал.
4. Изменяем режим наложения слоя Fast Retouch на Линейный свет. Мы должны увидеть размытую картинку.
5. Теперь снова размываем данный слой по Гауссу, только теперь с радиусом в 2-4 раза меньшим, проявляя мелкую текстуру кожи. Мы получим изображение, которое выглядит несколько необычно.
Мы получим изображение, которое выглядит несколько необычно.
6. Прячем данный слой в черную маску и белой кистью проявляем его в нужных местах. При этом избегайте работы вблизи контрастных границ, так как получите грязь на этих местах.
Впрочем, проблему грязи на контрастных границах довольно легко решить. Уже догадались как?
Правильно! Использовать для размытия фильтр, оставляющий четкие границы, например, Размытие по поверхности.
Достоинства метода: простота и эффективность, быстрота в применении для массовой обработки. В отличие от плагинов, более контролируемый результат.
Недостатки метода: отсутствие какой-либо гибкости в работе, невозможно получить результат высокого качества.
Многополосное разложение или «эквалайзер».
Для упрощения процесса ретуши можно модифицировать предыдущий метод, раскладывая изображение на несколько пространственных частот, с использованием различных радиусов для размытия изображения. Таким образом мы получим возможность, работая по маске слоя, быстро убирать дефекты различных размеров.
Таким образом мы получим возможность, работая по маске слоя, быстро убирать дефекты различных размеров.
Алгоритм создания эквалайзера:
1. Определяемся со значениями радиусов, которые будем использовать. Обычно используются значения 5, 10, 15, 25, 40 пикселей, но вы можете выбирать любые, которые вам подходят.
2. Создаем базовый слой, как в предыдущих методах.
3. Создаем необходимое количество копий, по числу радиусов плюс один слой. В данном случае шесть копий базового слоя.
4. Называем копии осмысленно, например, по диапазонам радиусов, то есть, 40, 40-25, 25-15, 15-10, 10-5, 5.
5. Отключаем все слои выше слоя 40. Размываем этот слой по Гауссу с радиусом 40 пикселей
6. Включаем вышележащий слой 40-25, переходим на него и выполняем вычитание слоя 40 с помощью команды Внешний канал.
7. Размываем данный слой по Гауссу с радиусом 25 пикселей. Получаем полосу частот от 40 до 25 пикселей.
Получаем полосу частот от 40 до 25 пикселей.
8. Меняем режим наложения на Линейный свет.
9. Переходим на слой 25-15 и, ВНИМАНИЕ! Не включаем видимость слоя!
10. Выполняем вычитание из данного слоя содержимого всех слоев. То есть, в настройках команды Внешний канал в качестве источника нужно поставить Объединено. Таким образом мы вычтем из данного слоя изображение, размытое на 25 пикселей.
11. Теперь включаем видимость слоя 25-15 и меняем режим наложения на Линейный свет.
12. Размываем слой 25-15 на 15 пикселей.
13. Повторяем операции с другими слоями. Последний слой, с названием 5, не размываем, так как на нем будет находиться текстура с размерами элементов до 5 пикселей.
14. Таким образом, мы получаем эквалайзер пространственных частот. Теперь мы можем как ослаблять нужный диапазон частот, так и усиливать его.![]() Ослабление производится путем наложения маски слоя и рисования по нужным местам черной кистью с необходимой непрозрачностью. Усиление производится с помощью корректирующего слоя, например, Кривые, действующего через обтравочную маску на конкретный слой. Поднимая контраст простым поворотом кривой против часовой стрелки, мы усиливаем контраст слоя, тем самым усиливая видимость данной полосы частот.
Ослабление производится путем наложения маски слоя и рисования по нужным местам черной кистью с необходимой непрозрачностью. Усиление производится с помощью корректирующего слоя, например, Кривые, действующего через обтравочную маску на конкретный слой. Поднимая контраст простым поворотом кривой против часовой стрелки, мы усиливаем контраст слоя, тем самым усиливая видимость данной полосы частот.
Достоинства метода: возможность быстрого подавления или усиления в выбранных полосах частот, таким образом можно значительно ускорить процесс ретуши.
Недостатки метода: сложность в реализации для начинающих, накопление ошибок округления из-за большого количества слоев, при работе вблизи контрастных границ те же проблемы с грязью из-за ореолов размытия.
Частотное разложение без потерь.
Все предыдущие способы разложения изображения на пространственные частоты имеют общий недостаток (хотя это скорее особенность), возникающий из-за целочисленной арифметики Photoshop, то есть, из-за округления чисел до целых при расчете.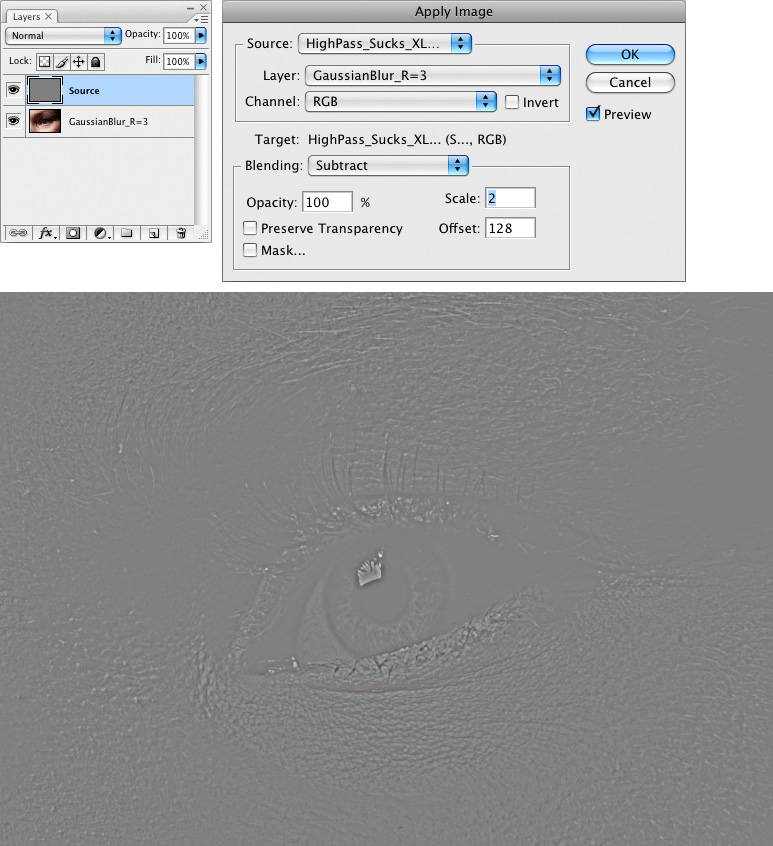 В результате, например, 5 разделить на 2 будет равно уже не 2.5, а 3.
В результате, например, 5 разделить на 2 будет равно уже не 2.5, а 3.
Поэтому, если вынести изображение, получаемое частотным разложением, на отдельный слой и сравнить его с исходником, наложив в режиме Разница (Difference) и сильно подняв контраст, мы увидим, что изображения имеют небольшое отличие друг от друга.
Как правило, это отличие не превышает один-два тоновых уровня. Те изменения, которые вносятся впоследствии в картинку при ретуши, несоизмеримо больше. Поэтому не следует обращать на это внимания.
Однако, если для вас все же критична даже такая микроскопическая разница, можете воспользоваться способом честного частотного разложения, без потерь.
Для режима 8 бит алгоритм будет следующий:
1. Создаем базовый слой. Делаем три копии базового слоя.
2. Называем первый слой Low, следующий High_Dark, и верхний High_Light.
3. Отключаем видимость слоев High_Light и High_Dark.
4. Размываем слой Low с необходимым радиусом. При этом можно использовать любые фильтры размытия.
5. Включаем слой High_Dark. Переходим на него. Применяем команду Внешний канал со следующими настройками: источник слой Low, канал RGB, инвертировать, режим наложения Линейный осветлитель (Linear Dodge).
6. Меняем режим наложения слоя High_Dark на Линейный затемнитель (Linear Burn).
7. Включаем слой High_Light и переходим на него. Применяем команду Внешний канал со следующими настройками: источник слой Low, канал RGB, инвертировать, режим наложения Линейный затемнитель.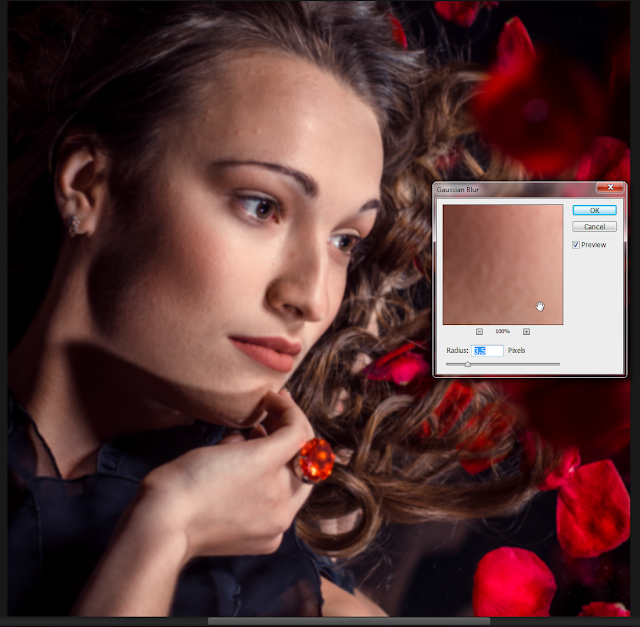
8. Меняем режим наложения слоя High_Light на Линейный осветлитель.
Если вынести разложенную картинку на отдельный слой с помощью комбинации клавиш CTRL+ALT+SHIFT+E, то при наложении ее на исходную в режиме Разница, с предельно усиленным контрастом, мы ничего не увидим. То есть, метод обеспечивает математически точное частотное разложение. К сожалению, в режиме 16 бит данный метод имеет видимую погрешность. Для 16 бит используется несколько другой алгоритм, который также дает погрешность, но уже на уровне единичных пикселей, что абсолютно некритично.
9. Таким образом, мы получаем два слоя для текстуры – один High_Light со светлой составляющей на черном фоне и второй High_Dark с темной составляющей на белом фоне. Ретушь текстуры в данном случае придется производить в два этапа, сначала одну составляющую, затем другую.
Достоинства метода: математически точное частотное разложение, без погрешностей.
Недостатки метода: необходимость ретуши высокочастотной составляющей в два этапа.
Алгоритм визуализации высокочастотной составляющей.
При работе с фильтрами размытия, такими как Размытие по поверхности (Surface Blur) или Медиана (Median) имеется определенная проблема. Заключается она в том, что довольно часто хочется реализовать видимость высокочастотной составляющей, как будто мы применяем фильтр Цветовой контраст. Это необходимо для того, чтобы иметь возможность контролировать, какая текстура будет впоследствии вынесена на высокочастотный слой.
Для визуализации высокочастотной составляющей я предложил следующий метод, который основан на знании математики режимов наложения и особенностей работы фильтров в Photoshop. Теперь этот метод используют многие ретушеры и преподаватели в различных онлайн и оффлайн школах, обучающих обработке изображений.
Алгоритм визуализации следующий:
1. Создаем базовый слой. Делаем две копии, называем одну Low, другую High. Слой High отключаем.
2. Копируем слой Low, называем копию Temp, что означает временный.
3. Слой Temp инвертируем и устанавливаем непрозрачность 50%. Получаем 50% серый.
4. Теперь над слоем Temp создаем временный корректирующий слой Инверсия (Invert).
5. Для дополнительного усиления контраста, чтобы лучше видеть текстуру, желательно создать еще один временный корректирующий слой Кривые, закрутив кривую RGB против часовой стрелки вокруг центральной точки.
6. Теперь, если мы будем размывать каким-либо фильтром слой Low, мы увидим серую картинку с текстурой, как будто мы применяем фильтр Цветовой контраст. В данном случае я применил фильтр Медиана
7. Подобрав таким образом параметры фильтра, применяем его, удаляем все временные слои.
Подобрав таким образом параметры фильтра, применяем его, удаляем все временные слои.
8. Затем включаем слой High и получаем высокочастотную составляющую путем вычитания с помощью команды Внешний канал.
Надеюсь, что данный сборник рецептов поможет вам лучше разобраться в использовании метода частотного разложения для ретуши в различных его вариациях.
Более подробно о самых современных методиках быстрой ретуши вы можете узнать из записи онлайн-мастер-класса «Частотное разложение 2.0. Эксклюзивные методики быстрой ретуши» (предупреждаю, что материал там не для начинающих).
А для тех, кто делает только первые шаги в ретуши, рекомендую запись моего трехдневного онлайн-марафона по ретуши «Сделай первые шаги в ретуши портретов»
По всем вариантам частотного разложения вы можете записать экшены и использовать их в своей работе. Пусть это будет вашим домашним заданием.
Автор: Евгений Карташов
05/01/2014
Просмотров : 556207
Источник: photo-monster. ru
ru
Автор: Евгений Карташов
Частотное разложение в Фотошопе (Полный урок)
Всем привет на уроке от WiFiGiD.RU. Сегодня мы поговорим про частотное разложение фотографии в Фотошопе. Для начала давайте я коротко расскажу, что это за зверь такой.
Частотное разложение изображения – процедура при которой текстура рисунка отделяется от слоя с оттенком и другими цветовыми тонами.
Очень часто используется при обработке портретных фото. При работе с частотным разложением у нас будет два слоя. Первый (верхний) – слой текстуры кожи и других поверхностей. Второй (нижний или фоновый) – будет содержать информацию только о тоне и цвете.
Для чего это нужно? При работе с двумя слоями, которые отвечают за разного рода информацию, проще обрабатывать очень сложные в структуре фотографии. Таким образом можно добавить максимального реализма при серьезной обработке.
Подобная процедура часто используется при создании объемных текстур в играх и 3D-анимации.
В уроке ниже мы пошагово и на русском языке посмотрим, как правильно делать частотное разложение в программе Фотошоп. Если в процессе возникнут какие-то вопросы – пишите в комментариях.
Содержание
- ШАГ 1: Создание дополнительных слоев
- ШАГ 2: Правка текстуры
- ШАГ 3: Исправление тона
- Задать вопрос автору статьи
ШАГ 1: Создание дополнительных слоев
Давайте на конкретном примере познакомимся с методом частотного разложения в Фотошопе. Для урока я взял фотографию глаз девушки. Наша задача: частично убрать некоторые погрешности. Конечно, мы можем начать использовать «Восстанавливающую кисть», но в таком случае обработка будет слишком грубая.
- В первую очередь нам нужно создать две копии нашей основной картинки. Для этого два раза используем горячие клавиши:
Ctrl + J
- Верхний слой у нас будет «Текстура», а нижний «Тон».
 Основной «Фон» – это изначальная картинка, мы будем периодически к ней обращаться для сравнения результата.
Основной «Фон» – это изначальная картинка, мы будем периодически к ней обращаться для сравнения результата.
- Выключаем отображение текстурного слоя и переходим на слой «Тон».
- Напомню, что на слое «Тон» у нас не должно быть никакой текстуры и должен быть только цвет. Для этого в разделе «Фильтр» находим «Размытие». Проще всего использовать «Размытие по Гауссу».
- Выставите такое значение, чтобы полностью пропала текстура и остался только цвет. Значение может быть больше или меньше в зависимости от разрешения изображения. Поэтому смотрите и устанавливайте значение на глаз. Обязательно запомните то число, которого установили (нам оно еще понадобится).
- Перейдите теперь на вкладку «Текстура» и примените «Фильтр» – «Краевой контраст» (может находиться на вкладке «Другое»). На старых версиях Photoshop может называться как «Цветовой контраст».
- Выставляем такое же значение как при размытии.

- Находясь на том же самом слое, выставите режим «Яркий свет».
Далее вы должны увидеть такую картинку как на «Фоне». Чтобы быстро проверить сходство, зажмите клавишу Alt и кликните левой кнопкой мыши по глазу рядом с «Фоном».
Скорее всего, вы увидите, что наше изображение с тоном и текстурой немного более контрастное. Чтобы немного подправить картинку, находясь в «Текстуре», добавьте «Кривые».
Ваша задача немного поднять левую грань и опустить правую. Теперь снова сравниваем с фоном, как мы это делали ранее. Нужно добиться примерно такого же результата как на изначальном изображении (Фон).
ШАГ 2: Правка текстуры
На самом деле частотное разложение мы выполнили, но давайте я покажу вам как с этими изображениями работать. Выключите отображение всех слоев кроме «Текстур».
Найдите инструмент «Восстанавливающая кисть» и используйте её.
Нам нужно на текстуре убрать на лице девушки все дефекты, прыщики угри и т. д. Выберите подходящий размер кисти таким образом, чтобы вы могли полностью «закрасить» все дефекты.
д. Выберите подходящий размер кисти таким образом, чтобы вы могли полностью «закрасить» все дефекты.
На лице находим участок чистой кожи с текстурой, зажимаем клавишу Alt и, не отпуская, её кликаем мышью по этому участку.
Теперь если вы будете рисовать, то кисть будет брать текстуру отсюда. Внимательно закрасьте все дефекты. Будьте очень аккуратны, чтобы текстура была равномерная.
ШАГ 3: Исправление тона
Кожу мы сделали идеальной, но теперь наша задача исправить некоторые моменты на слое «Тон». Выключите отображение «Текстуры» и перейдите слой с цветом тона.
На данном слое вы можете заметить пятна, которые остались после смазывания. Их лучше убрать.
Для закрашивания используем «Кисть».
Выберите мягкую кисточку, чтобы при закрашивании не было резких переходов, а закрашенные места не смотрелись дополнительными пятнами.
И осталось самое главное – аккуратно закрасить все яркие пятна на лице. Сама инструкция будет такая:
- Зажимаем клавишу Alt.

- Автоматически выберется инструмент «Пипетка». Не отпуская кнопку на клавиатуре, кликаем по тому месту, где идет равномерный цвет кожи рядом с пятном (более светлая часть).
- Отпускаем клавишу Alt
- Возвращается инструмент «Кисть». Теперь аккуратно закрашиваем пятно.
Делаем все до тех пор, пока все яркие пятна не будут закрашены, а цвет кожи не станет равномерным. Самое главное делать все максимально аккуратно, чтобы сохранить тени и полутени лица. В самом конце можете сравнить результат с изначальным изображением (Фон).
Частотно-временное разложение — SEG Wiki
Содержание
- 1 Преобразование Фурье
- 2 Частотно-временное представление
- 3 Продолжить изучение
- 4 Автор, ответственный за переписку
- 5 Благодарностей
- 6 Внешние ссылки
Рассмотрим форму волны или сигнала s как функцию времени t . Например, синусоида с некоторой амплитудой a и с некоторой частотой f может быть определен как
s (t) = asin (2πft) {\ displaystyle s (t) = a \ sin (2 \ pi ft)}.
Мы можем реализовать эту математическую функцию как подпрограмму, обычно также называемую функцией , на языке программирования Python. Поскольку компьютеры живут в дискретном мире, мы
необходимо оценить функцию в течение некоторого времени и с некоторой частотой дискретизации:
по определению sine_wave(f, a, продолжительность, частота дискретизации):
t = np.arange(0, продолжительность, 1/sample_rate)
вернуть * np.sin (2 * np.pi * f * t), т Теперь мы можем вызвать эту функцию, передав ей частоту f = 261,63 Гц. Мы попросим 0,25 с с частотой дискретизации 10 кГц.
с, t = sine_wave(f=261,63,
а=1,
продолжительность=0,25,
sample_rate=10e3) Это приводит к следующему сигналу, обычно называемому временным рядом , который мы визуализируем путем построения графика s в зависимости от времени t :
Я изобразил результирующий массив в виде линии, но на самом деле это ряд дискретных точек, представленных в Python в виде массива чисел, начиная с этих четырех:
array([ 0., 0.1636476 , 0.32288289, 0.47341253])
Построим первые 80 точек:
Когда воздух вибрирует на этой частоте, мы слышим среднее До или До4. Вы можете прослушать примечание для себя в Jupyter Notebook, сопровождающем эту статью, по адресу https://github.com/seg/tutorials-2018.
(Блокнот также содержит весь код для создания графиков.) Код для вывода массива s в виде звука очень короткий:
из IPython.display import Audio фс = 10e3 Аудио(и, скорость=fs)
Этот сигнал длится всего 0,25 с, а покачиваний уже много. Мы бы хотели иметь сейсмические данные на этой частоте! Большинство сейсмических данных воспроизводятся только на нижних 20–30 клавишах 88-клавишного фортепиано — действительно, самая нижняя клавиша — это A0, что на частоте 27,5 Гц превышает пиковую частоту многих старых съемок.
Если бы мы хотели узнать частоту этого сигнала, мы могли бы предположить, что это чистый тон, и просто подсчитать количество циклов в единицу времени. Но естественные сигналы редко бывают монотонными, так что давайте сделаем более интересный сигнал. Мы можем использовать нашу функцию, чтобы создать до-мажорный аккорд с тремя нотами (C4, E4 и G4), передав векторы-столбцы (изменив форму массивов) для частоты 9.0021 f и амплитуда a :
Мы можем использовать нашу функцию, чтобы создать до-мажорный аккорд с тремя нотами (C4, E4 и G4), передав векторы-столбцы (изменив форму массивов) для частоты 9.0021 f и амплитуда a :
f = np.массив ([261,6, 329,6, 392,0])
а = np.массив ([1,5, 0,5, 1])
s, t = sine_wave (f = f.reshape (3, 1),
а=а.изменить(3, 1),
продолжительность=0,25,
sample_rate=10e3) Результатом является набор из трех синусоидальных кривых длиной 0,25 с:
Общий сигнал определяется суммой трех кривых:
s = np.sum(s, axis=0)
Преобразование Фурье
Хотя это смешанное или политонный сигнал представляет собой просто сумму трех чистых тонов, разобраться в компонентах уже не тривиально. Здесь в дело вступает преобразование Фурье.
Мы не будем вдаваться в подробности того, как работает преобразование Фурье. Лучшее объяснение, которое я видел за последнее время, — это вводное видео Гранта Сандерсона. Дело в том, что преобразование описывает сигналы как смеси периодических составляющих. Попробуем на нашем аккорде.
Дело в том, что преобразование описывает сигналы как смеси периодических составляющих. Попробуем на нашем аккорде.
Сначала мы конусность сигнала путем умножения его на функцию окна . Идеальные чистые тона имеют бесконечную продолжительность, а сужение помогает предотвратить влияние краев нашего конечного сигнала на преобразование Фурье.
s = s * np.blackman(s.size)
Оконная функция (зеленая) оказывает сужающее действие на сигнал:
Поскольку функция s определена для данного момента времени t , мы называем это представление сигнала временем 9(е) {\ Displaystyle {\ шляпа {s}} (е)}). Это новое представление называется частотной областью. Он состоит из массива коэффициентов Фурье :
S = np.fft.fft(s)
Вспомогательная функция fftfreq() возвращает массив частот, соответствующих коэффициентам. Интервал выборки частоты определяется длительностью сигнала с : чем длиннее сигнал, тем меньше интервал выборки частоты. (Точно так же короткие интервалы выборки по времени соответствуют широкой полосе пропускания по частоте.)
Интервал выборки частоты определяется длительностью сигнала с : чем длиннее сигнал, тем меньше интервал выборки частоты. (Точно так же короткие интервалы выборки по времени соответствуют широкой полосе пропускания по частоте.)
freq = np.fft.fftfreq(s.size, d=1/10e3)
Результатом является массив из коэффициентов Фурье , большинство из которых равны нулю. Но на частотах аккорда и вблизи них коэффициенты велики. Результат: «рецепт» аккорда с точки зрения синусоидальных монотонов.
Это называется спектром сигнала s . Он показывает величину каждой частотной составляющей.
Частотно-временное представление
Теперь мы знаем, как расплетать политонические сигналы, но давайте введем еще одно усложнение — сигналы, компоненты которых меняются со временем. Такие сигналы называются нестационарный . Например,
подумайте о монотонном сигнале, тон которого меняется в какой-то момент (см. Блокнот для кода, который генерирует этот сигнал):
Мы можем вычислить преобразование Фурье этого сигнала, как и раньше:
с *= np.blackman(s.size) S = np.fft.fft(s) freq = np.fft.fftfreq(s.size, d=1/10e3)
И постройте амплитуду S в зависимости от массива частот freq :
Он очень похож на спектр, который мы сделали раньше, но без средней частоты. Пики немного более рассредоточены, потому что продолжительность каждого сигнала вдвое меньше, чем была.
(Общий принцип неопределенности распространяет сигналы по частоте по мере того, как они становятся более компактными во времени.)
Дело в том, что нет большой разницы между спектром двух смешанных сигналов и спектром двух последовательных сигналов. Если мы заботимся о локализации сигналов во времени
(мы делаем!), это проблема. Одним из решений является обращение к частотно-временным представлениям . Пытаясь разделить сигнал одновременно по времени и частоте, они предлагают способ одновременного использования преимуществ обеих областей.
Библиотека для построения графиков Python matplotlib предлагает удобный способ построения графика время-частота, также известного как спектрограмма . В одной строке кода он создает график 2D-изображения, показывающий зависимость частоты от времени.
В одной строке кода он создает график 2D-изображения, показывающий зависимость частоты от времени.
_ = plt.specgram(s, Fs=1/10e3,
NFFT=512, noverlap=480) Немного поработав, мы можем получить очень богатое представление наших данных:
График использует алгоритм, называемый кратковременным преобразованием Фурье, или STFT. Это просто делает преобразование Фурье в скользящем окне длиной NFFT с перекрытием точек, перекрывающихся в предыдущем окне. Мы хотим NFFT должен быть длинным, чтобы получить хорошее разрешение по частоте, и мы хотим, чтобы nooverlap был большим, чтобы получить хорошее разрешение по времени.
Обратите внимание, что мы не можем точно увидеть точную частоту компонентов — они не служат достаточно долго, чтобы их можно было зафиксировать. И есть некоторая неопределенность в отношении сроков перехода,
потому что для получения приличного разрешения по частоте нам нужен длинный сегмент сигнала (в данном случае 512 отсчетов) — поэтому мы теряем информацию о времени. Но в целом этот сюжет лучше, чем
Но в целом этот сюжет лучше, чем
только спектр: мы видим, что есть по крайней мере два сильных сигнала с частотами около 250 и 400 Гц, и что изменение происходит примерно через 0,125 с.
Фрагмент фортепианной музыки может напоминать такой сюжет. Поскольку клавиши пианино могут воспроизводить только одну ноту, спектрограмма фортепианной музыки выглядит как серия горизонтальных линий:
Существует большое сходство между этим частотно-временным разложением и нотной записью:
Оказывается, самые интересные сигналы — и, возможно, все естественные сигналы — политонны и нестационарны. По этой причине, хотя временные ряды часто полезны, частотно-временная декомпозиция может быть очень показательной. Вот некоторые примеры; в каждом случае частота отложена по вертикальной оси, а время по горизонтальной оси. Цвета указывают мощность от низкой (синий) до высокой (желтый) (пропорционально квадрату амплитуды).
Человеческий голос произносит «SEG». Сонорные гласные имеют гармоники (горизонтальные полосы), а шипящие звуки «С» и первой части «Г» — шумоподобные.
спектральные отклики.
На этой спектрограмме показана 5-секундная серия чириканий летучих мышей. Я указал 18 кГц, приблизительный предел человеческого слуха, оранжевой линией, и если вы слушаете звук этого сигнала в
Ноутбук, можно убедиться, что чириканье еле слышно при нормальной скорости воспроизведения; только при замедлении клипа они могут быть отчетливо слышны.
Наконец, вот вулканический «крик» — гармонический толчок, предшествующий взрывному извержению на горе Редут, Аляска, в марте 2009 года. На слух это звучит невероятно, но спектрограмма
тоже интересно. В отличие от чириканья летучей мыши, этот 15-минутный временной ряд нужно ускорить, чтобы его услышать.
Продолжить изучение
Все рисунки в этой записной книжке можно воспроизвести с помощью кода в записной книжке Jupyter, прилагаемой к этой статье, на https://github.com/seg/tutorials-2018. Вы даже можете запустить код в облаке и поиграть с ним в браузере. Ничего не сломаешь — не волнуйся!
В хранилище вы также найдете больше сигналов, синтетических и естественных, от сердцебиения и загадочного подводного щебетания до гравитационных волн и сейсмических следов. Мало того, есть записная книжка, показывающая, как использовать другой алгоритм — непрерывное вейвлет-преобразование — для проведения частотно-временного анализа другого типа.
Мало того, есть записная книжка, показывающая, как использовать другой алгоритм — непрерывное вейвлет-преобразование — для проведения частотно-временного анализа другого типа.
Счастливого разложения!
Автор, ответственный за переписку
- Автор, ответственный за переписку: Matt Hall, Agile Scientific, Mahone Bay, Новая Шотландия, Канада. Электронная почта:
mattagilescientific.com
Благодарности
Фортепианная запись из BWV846 Баха лицензирована Кимико Ишизака CC-BY на http://welltemperedclavier.org. Данные чириканья летучих мышей лицензированы CC-BY-NC пользователем http://freesound.org klankschap. Спасибо Алисии Хотовек-Эллис за ее помощь с данными о горе Редут, записанными вулканической обсерваторией Геологической службы США на Аляске.
Внешние ссылки
| найти литературу о Частотно-временное разложение |
- Мадагаскарский рабочий процесс — воспроизводимый с помощью Мадагаскарского программного обеспечения с открытым исходным кодом
Частотно-временная декомпозиция — SEG Wiki
Рассмотрим форму волны или сигнала s как функцию времени t . Например, синусоидальная волна с некоторой амплитудой a и с некоторой частотой f может быть определена как
Например, синусоидальная волна с некоторой амплитудой a и с некоторой частотой f может быть определена как
s (t) = asin (2πft) {\ displaystyle s (t) = a \ sin (2 \ pi ft)}.
Мы можем реализовать эту математическую функцию как подпрограмму, обычно также называемую функцией , на языке программирования Python. Поскольку компьютеры живут в дискретном мире, мы
необходимо оценить функцию в течение некоторого времени и с некоторой частотой дискретизации:
по определению sine_wave(f, a, продолжительность, частота дискретизации):
t = np.arange(0, продолжительность, 1/sample_rate)
return a * np.sin(2 * np.pi * f * t), t Теперь мы можем вызвать эту функцию, передав ей частоту f = 261,63 Гц. Мы попросим 0,25 с с частотой дискретизации 10 кГц.
с, t = sine_wave(f=261,63,
а=1,
продолжительность=0,25,
sample_rate=10e3) Это приводит к следующему сигналу, обычно называемому временной ряд , который мы визуализируем путем построения графика s в зависимости от времени t :
Я изобразил результирующий массив в виде линии, но на самом деле это ряд дискретных точек, представленных в Python в виде массива чисел, начиная с этих четырех:
array([ 0., 0.1636476 , 0.32288289, 0.47341253])
Построим первые 80 точек:
Когда воздух вибрирует на этой частоте, мы слышим среднее До или До4. Вы можете прослушать примечание для себя в Jupyter Notebook, сопровождающем эту статью, по адресу https://github.com/seg/tutorials-2018.
(В блокноте также содержится весь код для построения графиков.) Код для отображения массива s , так как звук очень короткий:
из IPython.display import Audio фс = 10e3 Audio(s, rate=fs)
Этот сигнал имеет длину всего 0,25 с, а шевелений уже много. Мы бы хотели иметь сейсмические данные на этой частоте! Большинство сейсмических данных воспроизводятся только на нижних 20–30 клавишах 88-клавишного фортепиано — действительно, самая нижняя клавиша — это A0, что на частоте 27,5 Гц превышает пиковую частоту многих старых съемок.
Если бы мы хотели узнать частоту этого сигнала, мы могли бы предположить, что это чистый тон, и просто подсчитать количество циклов в единицу времени.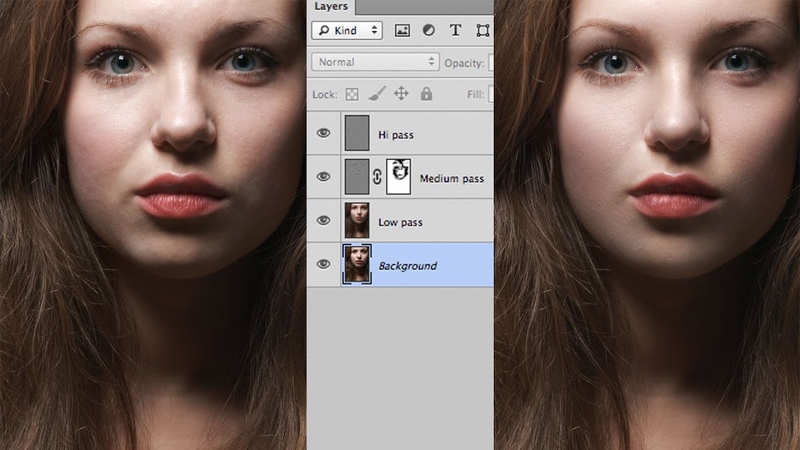 Но естественные сигналы редко бывают монотонными, так что давайте сделаем более интересный сигнал. Мы можем использовать нашу функцию, чтобы создать до-мажорный аккорд с тремя нотами (C4, E4 и G4), передав векторы-столбцы (изменив форму массивов) для частоты 9.0021 f и амплитуда a :
Но естественные сигналы редко бывают монотонными, так что давайте сделаем более интересный сигнал. Мы можем использовать нашу функцию, чтобы создать до-мажорный аккорд с тремя нотами (C4, E4 и G4), передав векторы-столбцы (изменив форму массивов) для частоты 9.0021 f и амплитуда a :
f = np.массив ([261,6, 329,6, 392,0])
а = np.массив ([1,5, 0,5, 1])
s, t = sine_wave (f = f.reshape (3, 1),
а=а.изменить(3, 1),
продолжительность=0,25,
sample_rate=10e3) Результатом является набор из трех синусоидальных кривых длиной 0,25 с:
Общий сигнал определяется суммой трех кривых:
s = np.sum(s, axis=0)
Преобразование Фурье
Хотя это смешанное или политонный сигнал представляет собой просто сумму трех чистых тонов, разобраться в компонентах уже не тривиально. Здесь в дело вступает преобразование Фурье.
Мы не будем вдаваться в подробности того, как работает преобразование Фурье.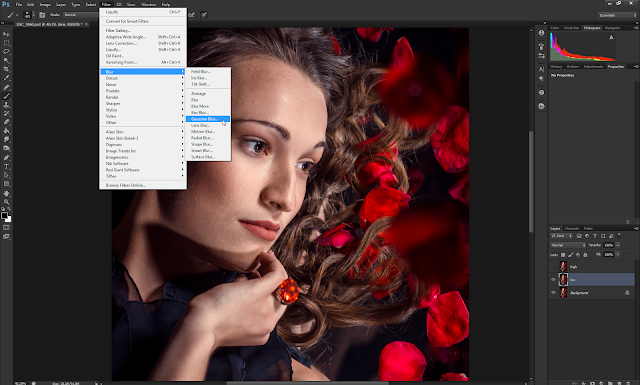 Лучшее объяснение, которое я видел за последнее время, — это вводное видео Гранта Сандерсона. Дело в том, что преобразование описывает сигналы как смеси периодических составляющих. Попробуем на нашем аккорде.
Лучшее объяснение, которое я видел за последнее время, — это вводное видео Гранта Сандерсона. Дело в том, что преобразование описывает сигналы как смеси периодических составляющих. Попробуем на нашем аккорде.
Сначала мы конусность сигнала путем умножения его на функцию окна . Идеальные чистые тона имеют бесконечную продолжительность, а сужение помогает предотвратить влияние краев нашего конечного сигнала на преобразование Фурье.
s = s * np.blackman(s.size)
Оконная функция (зеленая) оказывает сужающее действие на сигнал:
Поскольку функция s определена для данного момента времени t , мы называем это представление сигнала временем 9(е) {\ Displaystyle {\ шляпа {s}} (е)}). Это новое представление называется частотной областью. Он состоит из массива коэффициентов Фурье :
S = np.fft.fft(s)
Вспомогательная функция fftfreq() возвращает массив частот, соответствующих коэффициентам. Интервал выборки частоты определяется длительностью сигнала с : чем длиннее сигнал, тем меньше интервал выборки частоты. (Точно так же короткие интервалы выборки по времени соответствуют широкой полосе пропускания по частоте.)
Интервал выборки частоты определяется длительностью сигнала с : чем длиннее сигнал, тем меньше интервал выборки частоты. (Точно так же короткие интервалы выборки по времени соответствуют широкой полосе пропускания по частоте.)
freq = np.fft.fftfreq(s.size, d=1/10e3)
Результатом является массив из коэффициентов Фурье , большинство из которых равны нулю. Но на частотах аккорда и вблизи них коэффициенты велики. Результат: «рецепт» аккорда с точки зрения синусоидальных монотонов.
Это называется спектром сигнала s . Он показывает величину каждой частотной составляющей.
Частотно-временное представление
Теперь мы знаем, как расплетать политонические сигналы, но давайте введем еще одно усложнение — сигналы, компоненты которых меняются со временем. Такие сигналы называются нестационарный . Например,
подумайте о монотонном сигнале, тон которого меняется в какой-то момент (см. Блокнот для кода, который генерирует этот сигнал):
Мы можем вычислить преобразование Фурье этого сигнала, как и раньше:
с *= np.blackman(s.size) S = np.fft.fft(s) freq = np.fft.fftfreq(s.size, d=1/10e3)
И постройте амплитуду S в зависимости от массива частот freq :
Он очень похож на спектр, который мы сделали раньше, но без средней частоты. Пики немного более рассредоточены, потому что продолжительность каждого сигнала вдвое меньше, чем была.
(Общий принцип неопределенности распространяет сигналы по частоте по мере того, как они становятся более компактными во времени.)
Дело в том, что нет большой разницы между спектром двух смешанных сигналов и спектром двух последовательных сигналов. Если мы заботимся о локализации сигналов во времени
(мы делаем!), это проблема. Одним из решений является обращение к частотно-временным представлениям . Пытаясь разделить сигнал одновременно по времени и частоте, они предлагают способ одновременного использования преимуществ обеих областей.
Библиотека для построения графиков Python matplotlib предлагает удобный способ построения графика время-частота, также известного как спектрограмма . В одной строке кода он создает график 2D-изображения, показывающий зависимость частоты от времени.
В одной строке кода он создает график 2D-изображения, показывающий зависимость частоты от времени.
_ = plt.specgram(s, Fs=1/10e3,
NFFT=512, noverlap=480) Немного поработав, мы можем получить очень богатое представление наших данных:
График использует алгоритм, называемый кратковременным преобразованием Фурье, или STFT. Это просто делает преобразование Фурье в скользящем окне длиной NFFT с перекрытием точек, перекрывающихся в предыдущем окне. Мы хотим NFFT должен быть длинным, чтобы получить хорошее разрешение по частоте, и мы хотим, чтобы nooverlap был большим, чтобы получить хорошее разрешение по времени.
Обратите внимание, что мы не можем точно увидеть точную частоту компонентов — они не служат достаточно долго, чтобы их можно было зафиксировать. И есть некоторая неопределенность в отношении сроков перехода,
потому что для получения приличного разрешения по частоте нам нужен длинный сегмент сигнала (в данном случае 512 отсчетов) — поэтому мы теряем информацию о времени. Но в целом этот сюжет лучше, чем
Но в целом этот сюжет лучше, чем
только спектр: мы видим, что есть по крайней мере два сильных сигнала с частотами около 250 и 400 Гц, и что изменение происходит примерно через 0,125 с.
Фрагмент фортепианной музыки может напоминать такой сюжет. Поскольку клавиши пианино могут воспроизводить только одну ноту, спектрограмма фортепианной музыки выглядит как серия горизонтальных линий:
Существует большое сходство между этим частотно-временным разложением и нотной записью:
Оказывается, самые интересные сигналы — и, возможно, все естественные сигналы — политонны и нестационарны. По этой причине, хотя временные ряды часто полезны, частотно-временная декомпозиция может быть очень показательной. Вот некоторые примеры; в каждом случае частота отложена по вертикальной оси, а время по горизонтальной оси. Цвета указывают мощность от низкой (синий) до высокой (желтый) (пропорционально квадрату амплитуды).
Человеческий голос произносит «SEG». Сонорные гласные имеют гармоники (горизонтальные полосы), а шипящие звуки «С» и первой части «Г» — шумоподобные.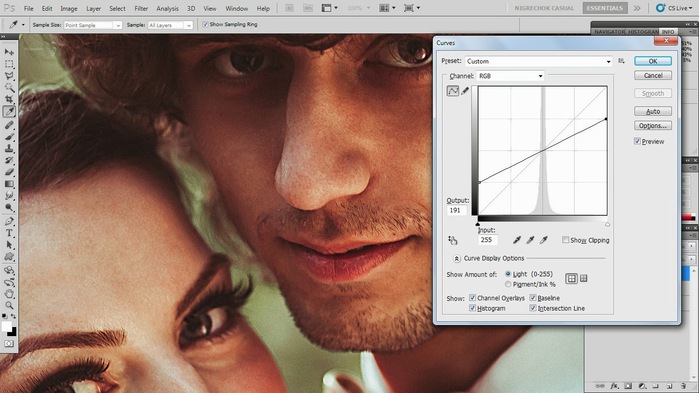
спектральные отклики.
На этой спектрограмме показана 5-секундная серия чириканий летучих мышей. Я указал 18 кГц, приблизительный предел человеческого слуха, оранжевой линией, и если вы слушаете звук этого сигнала в
Ноутбук, можно убедиться, что чириканье еле слышно при нормальной скорости воспроизведения; только при замедлении клипа они могут быть отчетливо слышны.
Наконец, вот вулканический «крик» — гармонический толчок, предшествующий взрывному извержению на горе Редут, Аляска, в марте 2009 года. На слух это звучит невероятно, но спектрограмма
тоже интересно. В отличие от чириканья летучей мыши, этот 15-минутный временной ряд нужно ускорить, чтобы его услышать.
Продолжить изучение
Все рисунки в этой записной книжке можно воспроизвести с помощью кода в записной книжке Jupyter, прилагаемой к этой статье, на https://github.com/seg/tutorials-2018. Вы даже можете запустить код в облаке и поиграть с ним в браузере. Ничего не сломаешь — не волнуйся!
В хранилище вы также найдете больше сигналов, синтетических и естественных, от сердцебиения и загадочного подводного щебетания до гравитационных волн и сейсмических следов.

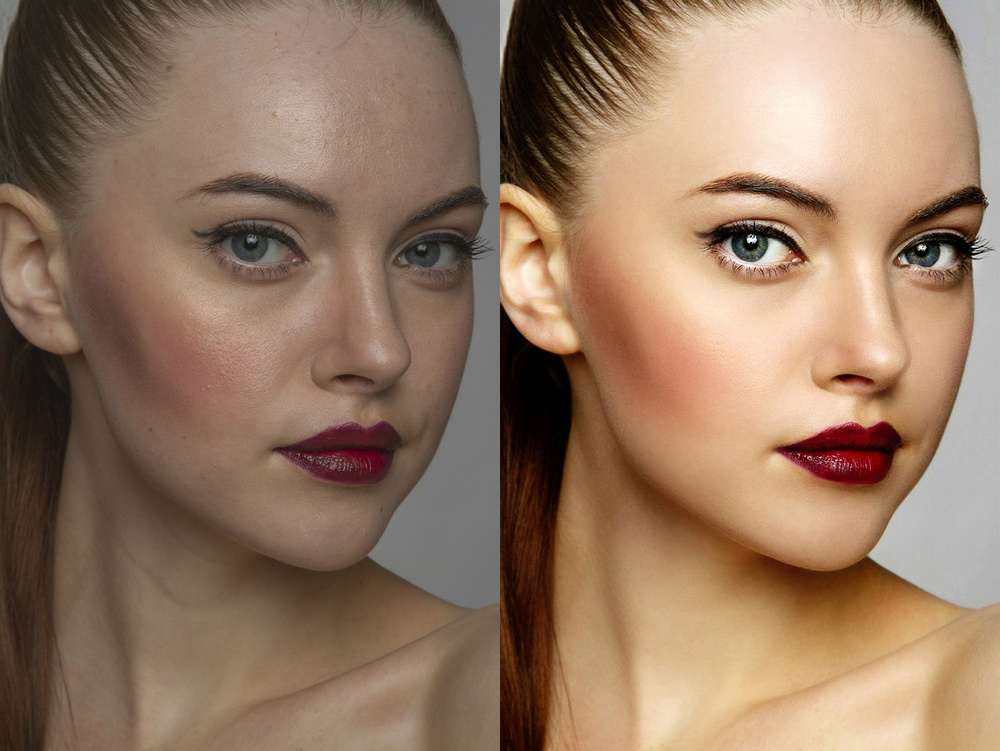 Подобная процедура часто используется при создании объемных текстур в играх и 3D-анимации.
Подобная процедура часто используется при создании объемных текстур в играх и 3D-анимации. Основной «Фон» – это изначальная картинка, мы будем периодически к ней обращаться для сравнения результата.
Основной «Фон» – это изначальная картинка, мы будем периодически к ней обращаться для сравнения результата.
 , 0.1636476 , 0.32288289, 0.47341253])
, 0.1636476 , 0.32288289, 0.47341253])  blackman(s.size)
S = np.fft.fft(s)
freq = np.fft.fftfreq(s.size, d=1/10e3)
blackman(s.size)
S = np.fft.fft(s)
freq = np.fft.fftfreq(s.size, d=1/10e3)  , 0.1636476 , 0.32288289, 0.47341253])
, 0.1636476 , 0.32288289, 0.47341253]) 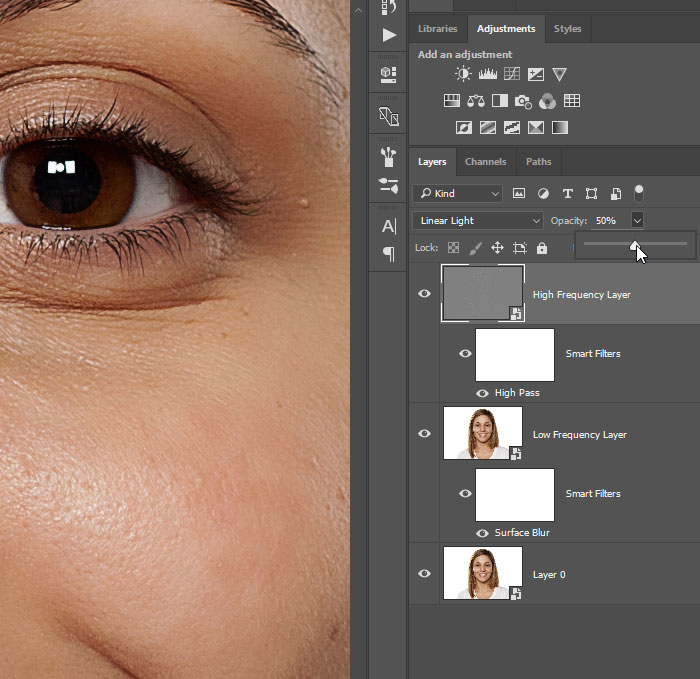 blackman(s.size)
S = np.fft.fft(s)
freq = np.fft.fftfreq(s.size, d=1/10e3)
blackman(s.size)
S = np.fft.fft(s)
freq = np.fft.fftfreq(s.size, d=1/10e3)  10.2021 5:11:40
10.2021 5:11:40 Эти профессиональные фоновые изображения для презентаций легко интегрируются в ваш дизайн. Итак, давайте проверим наши фоновые изображения PowerPoint PPT в HD качестве.
Эти профессиональные фоновые изображения для презентаций легко интегрируются в ваш дизайн. Итак, давайте проверим наши фоновые изображения PowerPoint PPT в HD качестве.




 Легальная оплата. Электронный чек.
Легальная оплата. Электронный чек.
 Однажды вы понимаете: времени у вас нет. И на глаза вдруг попадается эта малиновая кнопка…
Однажды вы понимаете: времени у вас нет. И на глаза вдруг попадается эта малиновая кнопка… Редактор вас поймёт и поддержит.
Редактор вас поймёт и поддержит. Задание 1.2
Задание 1.2 Такт. Размер
Такт. Размер Викторина 3
Викторина 3 12.15
12.15 Эта функция будет включена по умолчанию в Chrome 64 и более поздних версиях, но вы можете сразу же использовать ее с помощью флагов Chrome.
Эта функция будет включена по умолчанию в Chrome 64 и более поздних версиях, но вы можете сразу же использовать ее с помощью флагов Chrome. Кроме того, межсайтовые фреймы могут отображаться пустыми при печати веб-страницы. Чтобы обойти это, сохраните страницу локально, затем откройте и распечатайте сохраненный файл. Наконец, некоторые веб-сайты могут работать некорректно.
Кроме того, межсайтовые фреймы могут отображаться пустыми при печати веб-страницы. Чтобы обойти это, сохраните страницу локально, затем откройте и распечатайте сохраненный файл. Наконец, некоторые веб-сайты могут работать некорректно. Следите за ним в Твиттере.
Следите за ним в Твиттере.




 Можно сделать что-то шутливое или простое и милое.
Можно сделать что-то шутливое или простое и милое. Мы разработали специальные вертикальные шаблоны, чтобы видео, которым вы решили поздравить девушку с днём рождения, можно было опубликовать в социальных сетях.
Мы разработали специальные вертикальные шаблоны, чтобы видео, которым вы решили поздравить девушку с днём рождения, можно было опубликовать в социальных сетях. После сохранения и скачивания презентация на день рождения девушки остается неизменной, отредактировать ее не получится.
После сохранения и скачивания презентация на день рождения девушки остается неизменной, отредактировать ее не получится. Унесёт с лепесткомОдуванчика пусть!Ночь простит все слова.Бог простит…
Унесёт с лепесткомОдуванчика пусть!Ночь простит все слова.Бог простит… Вот некоторые из моих самых любимых идей видеопоздравлений на день рождения любимого человека.
Вот некоторые из моих самых любимых идей видеопоздравлений на день рождения любимого человека. Например, у твоего брата день рождения; попробуйте включить всех членов вашей семьи, поздравляющих его с днем рождения, одного за другим в видео и отправить ему. Это будет большим сюрпризом. Вы также можете добавить несколько текстов на видео, например, использовать дурацкие или забавные цитаты. Это может быть и забавно, и неприятно одновременно, и это обязательно осветит момент. Они могут быть такими:
Например, у твоего брата день рождения; попробуйте включить всех членов вашей семьи, поздравляющих его с днем рождения, одного за другим в видео и отправить ему. Это будет большим сюрпризом. Вы также можете добавить несколько текстов на видео, например, использовать дурацкие или забавные цитаты. Это может быть и забавно, и неприятно одновременно, и это обязательно осветит момент. Они могут быть такими: Постарайтесь сделать это забавным, чтобы вы использовали смех или два. Вы бы использовали кавычки, например:
Постарайтесь сделать это забавным, чтобы вы использовали смех или два. Вы бы использовали кавычки, например: Поэтому постарайтесь собрать как можно больше друзей, с которыми вы разделяете это воспоминание, и сделайте групповое видео, вспоминая старые времена и наслаждаясь счастьем момента.
Поэтому постарайтесь собрать как можно больше друзей, с которыми вы разделяете это воспоминание, и сделайте групповое видео, вспоминая старые времена и наслаждаясь счастьем момента. Я думаю, что пение для людей, которых ты любишь, заставит их полюбить тебя еще больше. Так почему бы вам не попробовать произвести на них впечатление их любимой песней, или вы можете просто использовать мелодию и написать текст самостоятельно, который идеально соответствует их индивидуальности. Это сделает его еще более интересным для просмотра и создания. Также можно немного потанцевать, только под биты.
Я думаю, что пение для людей, которых ты любишь, заставит их полюбить тебя еще больше. Так почему бы вам не попробовать произвести на них впечатление их любимой песней, или вы можете просто использовать мелодию и написать текст самостоятельно, который идеально соответствует их индивидуальности. Это сделает его еще более интересным для просмотра и создания. Также можно немного потанцевать, только под биты. д., но самое главное, скажите им, что вы гордитесь тем, что у вас есть такой особенный человек, как они.
д., но самое главное, скажите им, что вы гордитесь тем, что у вас есть такой особенный человек, как они. » неизвестный
» неизвестный  Ты всегда получаешь от меня лучшее. Я не знаю, как ты это делаешь, но я люблю тебя за это. С Днем Рождения.» неизвестный
Ты всегда получаешь от меня лучшее. Я не знаю, как ты это делаешь, но я люблю тебя за это. С Днем Рождения.» неизвестный  Вы не можете быть с ними любвеобильными, но, тем не менее, вы должны быть дружелюбны на пределе. Итак, попробуйте сделать видео с пожеланиями на день рождения, где вы желаете им, а также мотивируйте их на будущую тяжелую работу и на то, как иногда это может быть тяжело, но не сдавайтесь, и вы будете рядом с ними.
Вы не можете быть с ними любвеобильными, но, тем не менее, вы должны быть дружелюбны на пределе. Итак, попробуйте сделать видео с пожеланиями на день рождения, где вы желаете им, а также мотивируйте их на будущую тяжелую работу и на то, как иногда это может быть тяжело, но не сдавайтесь, и вы будете рядом с ними.
 Может быть, вы оба начинали так плохо, а потом узнали друг друга. Итак, поделитесь их первым впечатлением о вас и посмотрите, насколько это значимо.
Может быть, вы оба начинали так плохо, а потом узнали друг друга. Итак, поделитесь их первым впечатлением о вас и посмотрите, насколько это значимо. д. Вы можете сделать мини-биографические воспоминания из своего детства, чтобы представить вас обоих. Ваши трудности и моменты, когда вы были низки в жизни, и как вы их преодолели. Я уверен, что у вас есть много историй, которыми можно поделиться, так почему бы не начать одну за другой.
д. Вы можете сделать мини-биографические воспоминания из своего детства, чтобы представить вас обоих. Ваши трудности и моменты, когда вы были низки в жизни, и как вы их преодолели. Я уверен, что у вас есть много историй, которыми можно поделиться, так почему бы не начать одну за другой. Это, безусловно, будет эмоциональная поездка на американских горках, воспоминания о былых временах, глупые розыгрыши над соседями и т. д. Но постарайтесь вспоминать только хорошие времена, а не грустные, душераздирающие увлечения или что-то в этом роде.
Это, безусловно, будет эмоциональная поездка на американских горках, воспоминания о былых временах, глупые розыгрыши над соседями и т. д. Но постарайтесь вспоминать только хорошие времена, а не грустные, душераздирающие увлечения или что-то в этом роде.
 д. все смешно и сделать видео с приглашением их. Убедитесь, что видео и все остальное настолько идеально, насколько вы хотите, чтобы вечеринка прошла.
д. все смешно и сделать видео с приглашением их. Убедитесь, что видео и все остальное настолько идеально, насколько вы хотите, чтобы вечеринка прошла. Вы должны показать им, как все их ждут и как обстоят дела без них.
Вы должны показать им, как все их ждут и как обстоят дела без них. Вы также можете добавить музыку вместе с текстом!
Вы также можете добавить музыку вместе с текстом! На шаг ближе к трусам для взрослых.» Неизвестно.
На шаг ближе к трусам для взрослых.» Неизвестно. 

 С днем рождения!» Неизвестный.
С днем рождения!» Неизвестный.  Вы можете делать с этим программным обеспечением все, что захотите, от редактирования до добавления эффектов, текстов, аудио и т. д. Это программное обеспечение известно как iMyFone Filme.
Вы можете делать с этим программным обеспечением все, что захотите, от редактирования до добавления эффектов, текстов, аудио и т. д. Это программное обеспечение известно как iMyFone Filme.
 На верхней панели инструментов Filme есть опция звука.
На верхней панели инструментов Filme есть опция звука. Как бы вы ни отслеживали течение времени, 40-летие — это большое событие!
Как бы вы ни отслеживали течение времени, 40-летие — это большое событие!
 I.
I.  Если у вас есть фотографии, сопровождающие любое из этих достижений, обязательно покажите их при записи видеообращения.
Если у вас есть фотографии, сопровождающие любое из этих достижений, обязательно покажите их при записи видеообращения.


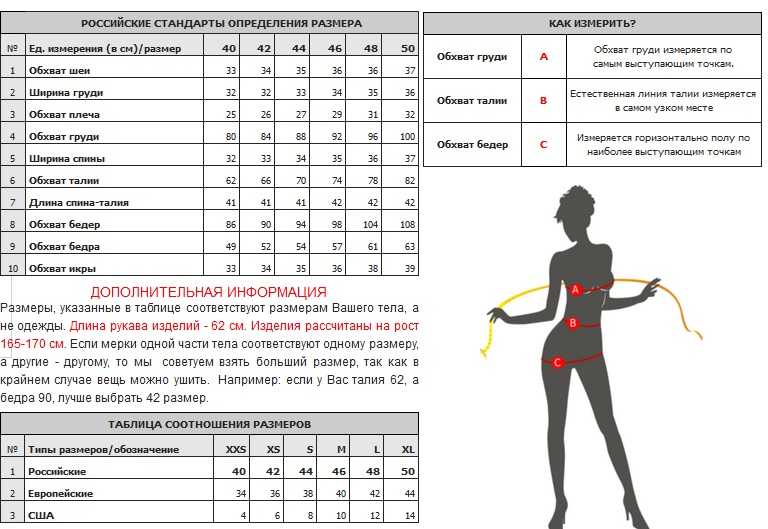 Можно пояснить термин или вообще его не использовать — просто написать, что ткань не даёт усадку.
Можно пояснить термин или вообще его не использовать — просто написать, что ткань не даёт усадку.


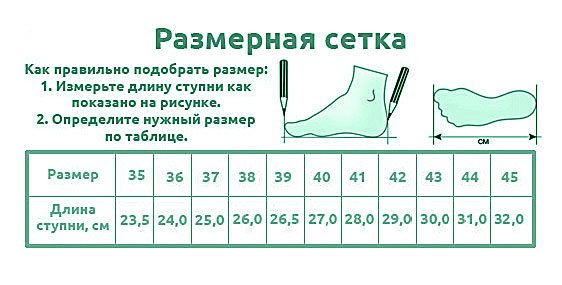 Подумайте, понравятся ли они целевой аудитории, подходят ли вашему товару.
Подумайте, понравятся ли они целевой аудитории, подходят ли вашему товару.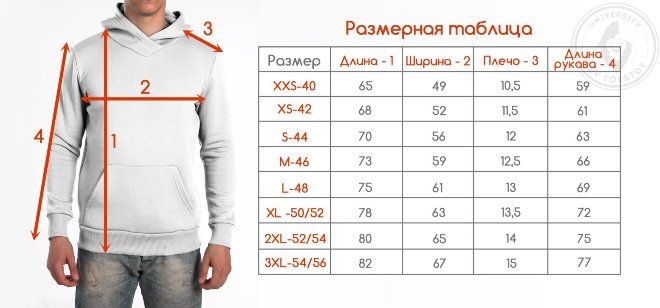
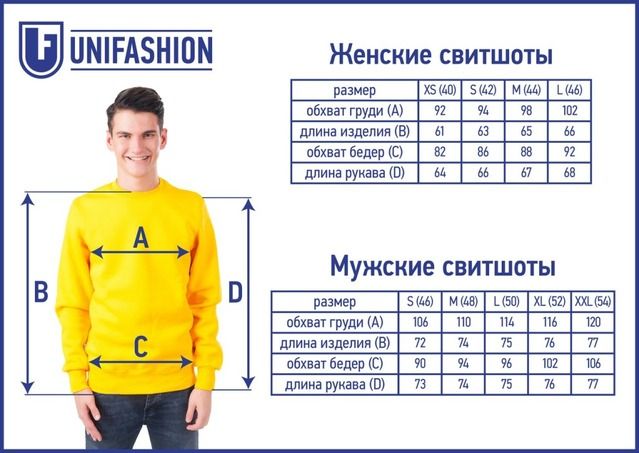
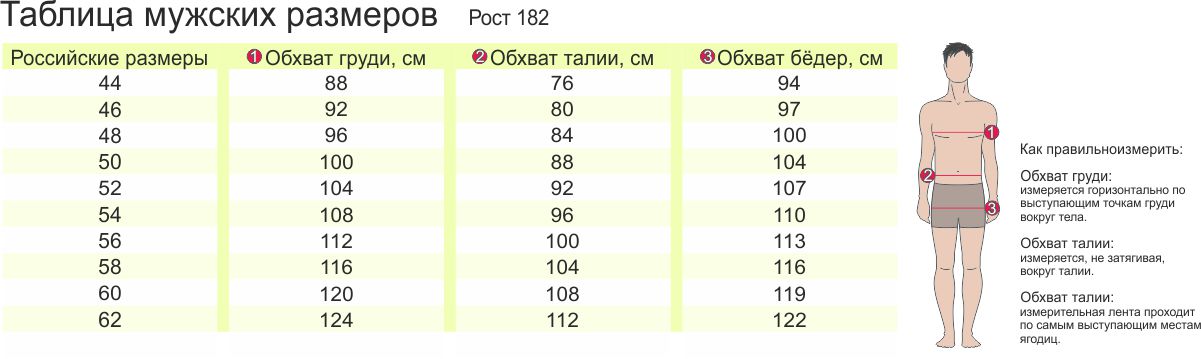 д.
д.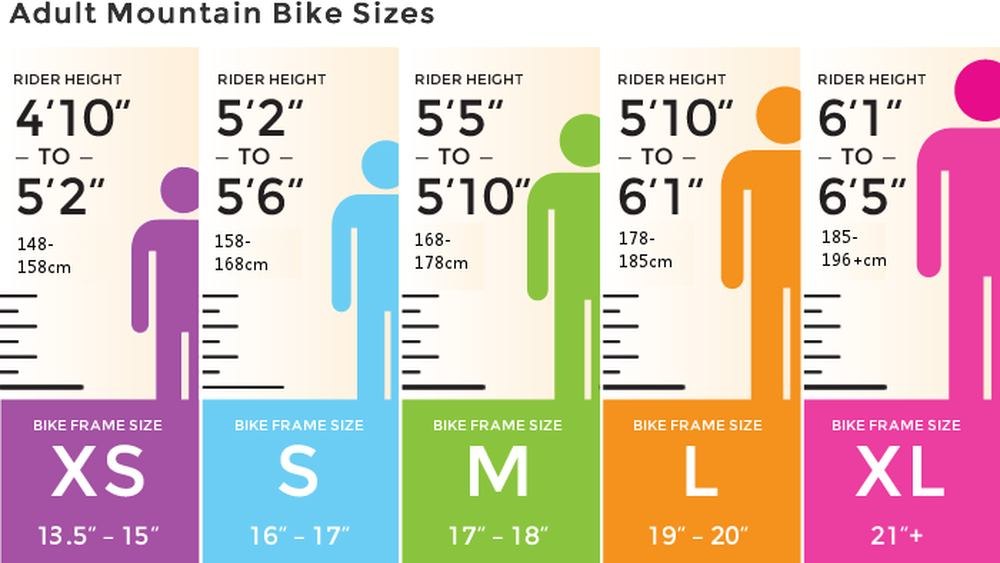
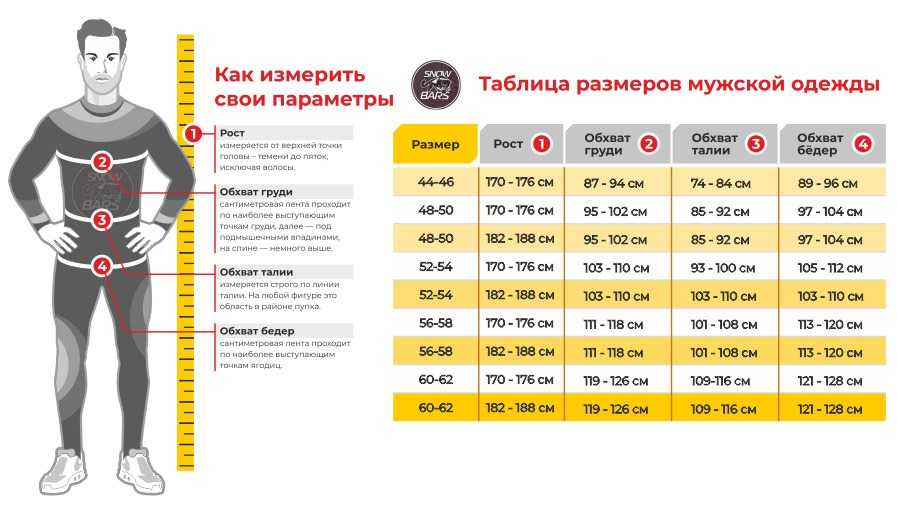 Инфографику можно использовать для рекламы, размещая на билбордах на дорогах. Их можно физически размещать в разных местах, чтобы повышать осведомленность о чем-то, заниматься политикой, обучать людей, заниматься бизнесом и т. д.
Инфографику можно использовать для рекламы, размещая на билбордах на дорогах. Их можно физически размещать в разных местах, чтобы повышать осведомленность о чем-то, заниматься политикой, обучать людей, заниматься бизнесом и т. д.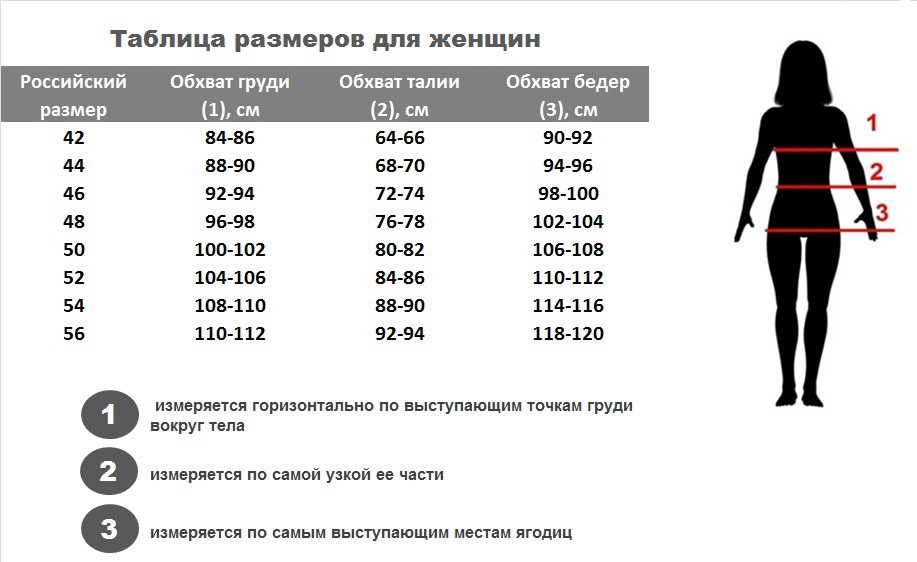 д.
д.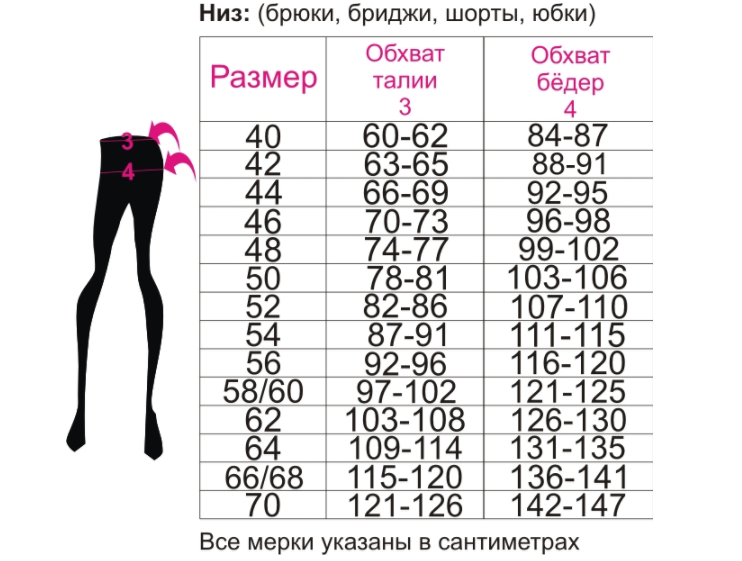 Вы должны увидеть, где вы разместите инфографику, или вы возьмете ее распечатку или разместите в Интернете? Тематика инфографики также различается по размеру.
Вы должны увидеть, где вы разместите инфографику, или вы возьмете ее распечатку или разместите в Интернете? Тематика инфографики также различается по размеру. Обратите внимание, что булавки организованы в столбцы, поэтому вертикальные булавки занимают больше места и, как правило, больше выделяются.
Обратите внимание, что булавки организованы в столбцы, поэтому вертикальные булавки занимают больше места и, как правило, больше выделяются.
 07KB
07KB 18MB
18MB 04KB
04KB 13MB
13MB 24KB
24KB 33KB
33KB 01KB
01KB Мужская рука на зеленом хромакее в виниле перчатки хорошо и недурно жест один щелчок keyingClose-вверх рука азиатского человека, показывая большой палец вверх знак жест, изолированные на фоне зеленого экрана цветности ключ. Набор из 4 жестов. Рекламный фон. Женская рука стирает пространство для копирования текста, изолированного на оранжевом.Chromakey. Зеленый экран. Женская рука на рок-концерте. Рога. Это качает.Chromakey. Зеленый экран. Мужская рука делает все в порядке. Мужской знак руки показывает палец вверх над зеленым экраном. Жесты женской руки. OKAY OK CLASS. Создавайте символы рукой на Greenscreen.4K кадры в режиме реального времени крупным планом азиатской молодой девушки, считающей от одного до пяти, изолированной на цветном ключе на зеленом фоне экрана. Хромакей. Женщина рука делает знак автостопом палец вверх большой палец вниз белый экранМужская рука поднимается вверх, показывая жест ок на зеленом хромакее, ввод одним нажатием
Мужская рука на зеленом хромакее в виниле перчатки хорошо и недурно жест один щелчок keyingClose-вверх рука азиатского человека, показывая большой палец вверх знак жест, изолированные на фоне зеленого экрана цветности ключ. Набор из 4 жестов. Рекламный фон. Женская рука стирает пространство для копирования текста, изолированного на оранжевом.Chromakey. Зеленый экран. Женская рука на рок-концерте. Рога. Это качает.Chromakey. Зеленый экран. Мужская рука делает все в порядке. Мужской знак руки показывает палец вверх над зеленым экраном. Жесты женской руки. OKAY OK CLASS. Создавайте символы рукой на Greenscreen.4K кадры в режиме реального времени крупным планом азиатской молодой девушки, считающей от одного до пяти, изолированной на цветном ключе на зеленом фоне экрана. Хромакей. Женщина рука делает знак автостопом палец вверх большой палец вниз белый экранМужская рука поднимается вверх, показывая жест ок на зеленом хромакее, ввод одним нажатием Стандартная лицензия охватывает большинство вариантов использования, включая рекламу и дизайн пользовательского интерфейса на веб-сайтах и в приложениях.
Стандартная лицензия охватывает большинство вариантов использования, включая рекламу и дизайн пользовательского интерфейса на веб-сайтах и в приложениях.

 Фото товаров тоже загружаются автоматически.
Фото товаров тоже загружаются автоматически. Если будет ошибка, маркетплейс не даст загрузить файл. Одну и ту же таблицу использовать не получится. Шаблоны часто меняют.
Если будет ошибка, маркетплейс не даст загрузить файл. Одну и ту же таблицу использовать не получится. Шаблоны часто меняют.


 Изменения моментально отправляются на маркетплейсы.
Изменения моментально отправляются на маркетплейсы. Функция пригодится, если у вас несколько ИП или юрлиц на одном маркетплейсе. Как это сделать, смотрите здесь.
Функция пригодится, если у вас несколько ИП или юрлиц на одном маркетплейсе. Как это сделать, смотрите здесь.
 Обычно именно такие форматы разрешены при загрузке изображений на популярные площадки. В последнее время на фоне большой конкуренции качество дизайна сильно возросло, поэтому уделяйте внимание качеству карточек.
Обычно именно такие форматы разрешены при загрузке изображений на популярные площадки. В последнее время на фоне большой конкуренции качество дизайна сильно возросло, поэтому уделяйте внимание качеству карточек. Иногда шрифт при этом сохраняет и значение, как бы, зашифрованного текста, подобно древнерусской вязи.
Иногда шрифт при этом сохраняет и значение, как бы, зашифрованного текста, подобно древнерусской вязи. Такое изображение строится не в глубину, а прямо на плоскости, вдоль которой направлено движение фигур. Фаворский, специально изучавший законы связи изображения со шрифтом, называл такую плоскость “двигательной” поверхностью.
Такое изображение строится не в глубину, а прямо на плоскости, вдоль которой направлено движение фигур. Фаворский, специально изучавший законы связи изображения со шрифтом, называл такую плоскость “двигательной” поверхностью.

 Бодони считается открывателем “новых антикв”, т.е. шрифтов с тонкими засечками, контрастностью. Уже при жизни Бодони считался ведущим в Европе мастером шрифта.
Бодони считается открывателем “новых антикв”, т.е. шрифтов с тонкими засечками, контрастностью. Уже при жизни Бодони считался ведущим в Европе мастером шрифта.
 Формы литер так же ценны, как графические элементы, поскольку они — графическое отображение языка, и заставить шрифт служить сразу нескольким целям в композиции — это надежный способ повысить качество вашей работы.
Формы литер так же ценны, как графические элементы, поскольку они — графическое отображение языка, и заставить шрифт служить сразу нескольким целям в композиции — это надежный способ повысить качество вашей работы. Приступим!
Приступим! Данная структура приводит к общему знаменателю обе части дизайна, несмотря на огромную разницу в стиле, перспективе и масштабе. Постеры в модернистском стиле часто имеют ключевой графический элемент или типографику и привязанный к ней шрифт, но я не видела, чтобы кому-то удавалось связать главные и второстепенные элементы так, как это делает Свендсен.
Данная структура приводит к общему знаменателю обе части дизайна, несмотря на огромную разницу в стиле, перспективе и масштабе. Постеры в модернистском стиле часто имеют ключевой графический элемент или типографику и привязанный к ней шрифт, но я не видела, чтобы кому-то удавалось связать главные и второстепенные элементы так, как это делает Свендсен. Ищите способы добавить разнообразия эстетическим элементам в вашей работе, и не забывайте строить мосты между задействованными стилями.
Ищите способы добавить разнообразия эстетическим элементам в вашей работе, и не забывайте строить мосты между задействованными стилями. Точки в курсиве идеально ровные и кажутся чересчур механическими и точными по сравнению с обтекаемостью остальной части надписи. И поскольку они выскакивают за верхний предел, то кажутся почти полностью оторванными от мелких строчных букв, утонувших внизу. Они озадачивают глаз — к какому шрифту это принадлежит? — и связывают два слоя, выступая одновременно в качестве элементов литер и точек в пространстве, объединяющих композицию. Это также хитрый способ ввести геометрию в строгий типографический дизайн, наравне с «+» и квадратным двоеточием. Вот ценное напоминание о том, что шрифты содержат великое множество символов, которые могут служить чисто графическим целям.
Точки в курсиве идеально ровные и кажутся чересчур механическими и точными по сравнению с обтекаемостью остальной части надписи. И поскольку они выскакивают за верхний предел, то кажутся почти полностью оторванными от мелких строчных букв, утонувших внизу. Они озадачивают глаз — к какому шрифту это принадлежит? — и связывают два слоя, выступая одновременно в качестве элементов литер и точек в пространстве, объединяющих композицию. Это также хитрый способ ввести геометрию в строгий типографический дизайн, наравне с «+» и квадратным двоеточием. Вот ценное напоминание о том, что шрифты содержат великое множество символов, которые могут служить чисто графическим целям. В результате получилось более чистое переднеплановое/фоновое отношение между двумя типами шрифтов, которое создает ощущение отполированности, в то же время сохраняя «ошибки» и беспорядочность, что позволяет избежать чрезмерной формализации. Это превосходный пример того, что называется «Making and Breaking the grid» («Создание и Разрушение сетки»). Те области, где шрифты сталкиваются и накладываются, наиболее эффектны благодаря сдержанности всех остальных частей постера.
В результате получилось более чистое переднеплановое/фоновое отношение между двумя типами шрифтов, которое создает ощущение отполированности, в то же время сохраняя «ошибки» и беспорядочность, что позволяет избежать чрезмерной формализации. Это превосходный пример того, что называется «Making and Breaking the grid» («Создание и Разрушение сетки»). Те области, где шрифты сталкиваются и накладываются, наиболее эффектны благодаря сдержанности всех остальных частей постера. Помните об этом мощном инструменте, когда комбинируете шрифты.
Помните об этом мощном инструменте, когда комбинируете шрифты. Прежде чем мы углубимся в это, давайте обсудим еще более основополагающее решение [дизайнера] — выровнять текст по правому краю. Если вы возьмете Maelstrom и нагромоздите литеры так же, как на фото, но слева (снизу, сильно слева), то останется какое-то ощущение неудовлетворенности, не так ли? Это создает много замкнутого пространства — слева от А и под хвостиком Y. Выравнивание по правому краю позволяет использовать гораздо более интересные области на полях, благодаря «ковшу», созданному Y, который загребает край, и A расширяющейся через несколько строк. Это скульптурирование также, вероятно, привело к решению оттянуть две последние строки текста от правого края — это единственный способ отделить A от L, находящейся над ней.
Прежде чем мы углубимся в это, давайте обсудим еще более основополагающее решение [дизайнера] — выровнять текст по правому краю. Если вы возьмете Maelstrom и нагромоздите литеры так же, как на фото, но слева (снизу, сильно слева), то останется какое-то ощущение неудовлетворенности, не так ли? Это создает много замкнутого пространства — слева от А и под хвостиком Y. Выравнивание по правому краю позволяет использовать гораздо более интересные области на полях, благодаря «ковшу», созданному Y, который загребает край, и A расширяющейся через несколько строк. Это скульптурирование также, вероятно, привело к решению оттянуть две последние строки текста от правого края — это единственный способ отделить A от L, находящейся над ней. Круглый значок Y застревает в H и предотвращает появление лишнего пустого пространства.
Круглый значок Y застревает в H и предотвращает появление лишнего пустого пространства.
 Я несколько раз использовала термин «скульптурирование», чтобы описать постер, и я думаю, это подходящее слово для описания типографики в целом. Каждый шрифт, даже идеальный — это только начальная точка. Как ее развить — решать вам.
Я несколько раз использовала термин «скульптурирование», чтобы описать постер, и я думаю, это подходящее слово для описания типографики в целом. Каждый шрифт, даже идеальный — это только начальная точка. Как ее развить — решать вам. Здесь шрифт имеет физическое присутствие в своей среде и использует идеи реального мира, чтобы повлиять на другой шрифт, усиливая смысл. Тривиально, но эффектно.
Здесь шрифт имеет физическое присутствие в своей среде и использует идеи реального мира, чтобы повлиять на другой шрифт, усиливая смысл. Тривиально, но эффектно. Эта техника создает скорее эффект взгляда «в», нежели «вверх», и это чаще всего достигается масштабированием и повторением одного и того же слова с каждой стороны. Повторение может быть мощным, но оно не позволяет использовать разные фразы и длины, как на постере 21 Урок.
Эта техника создает скорее эффект взгляда «в», нежели «вверх», и это чаще всего достигается масштабированием и повторением одного и того же слова с каждой стороны. Повторение может быть мощным, но оно не позволяет использовать разные фразы и длины, как на постере 21 Урок. Несмотря на то, что эта идея могла быть отражена с помощью обычной диаграммы — Дорфсман создавал похожую рекламу для других предметов, комбинируя изображения и графики — типографика великолепно транслирует месседж здесь.
Несмотря на то, что эта идея могла быть отражена с помощью обычной диаграммы — Дорфсман создавал похожую рекламу для других предметов, комбинируя изображения и графики — типографика великолепно транслирует месседж здесь. В этой истории не остается никаких сомнений насчет того, кто тут главный герой.
В этой истории не остается никаких сомнений насчет того, кто тут главный герой. Шрифт несет в себе столько смыслов, и в языке коммуникации и в форме дизайна. Когда соберетесь использовать фигуры или изображения, чтобы выразить мысль, бросьте себе вызов, попробуйте сделать это с помощью шрифта, и посмотрите, что из этого получится.
Шрифт несет в себе столько смыслов, и в языке коммуникации и в форме дизайна. Когда соберетесь использовать фигуры или изображения, чтобы выразить мысль, бросьте себе вызов, попробуйте сделать это с помощью шрифта, и посмотрите, что из этого получится.

 Маленькое количество элементов означает, что каждый из них должен быть очень весомым, и лучшие «простые» макеты — те, которые выжимают концептуальную и композиционную ценность из каждого звена до последней капли.
Маленькое количество элементов означает, что каждый из них должен быть очень весомым, и лучшие «простые» макеты — те, которые выжимают концептуальную и композиционную ценность из каждого звена до последней капли. Точно так же набор в три колонки без полей на примере справа — это очевидная отсылка к высоким стройным колоннам на фотографии, которую он [шрифт] сопровождает (здесь также есть нахальная отсылка к шляпе на противоположном развороте в заголовке в нижнем левом углу).
Точно так же набор в три колонки без полей на примере справа — это очевидная отсылка к высоким стройным колоннам на фотографии, которую он [шрифт] сопровождает (здесь также есть нахальная отсылка к шляпе на противоположном развороте в заголовке в нижнем левом углу).

 001/002/003
001/002/003 com
com
 Большинство его поклонников знают о его сольной музыке для саксофона и фортепиано, его классических квартетах, Ghost Trance Music, даже операх и пьесах для нескольких оркестров. Но даже среди знатоков остаются сюрпризы. Будь то его хореографический язык движений или интерактивная электроника, музыка для волынки, органов или угольных лопат, географические картографические системы или масштабные 8-часовые проекты Sonic Genome Projects, удовольствие от наблюдения за работами Энтони заключается в том, что сюрпризы никогда не прекращаются.
Большинство его поклонников знают о его сольной музыке для саксофона и фортепиано, его классических квартетах, Ghost Trance Music, даже операх и пьесах для нескольких оркестров. Но даже среди знатоков остаются сюрпризы. Будь то его хореографический язык движений или интерактивная электроника, музыка для волынки, органов или угольных лопат, географические картографические системы или масштабные 8-часовые проекты Sonic Genome Projects, удовольствие от наблюдения за работами Энтони заключается в том, что сюрпризы никогда не прекращаются. Когда я начал работать с Дэйвом Дугласом на Фестивале новой музыки для трубы (FONT), идея организовать концерт с участием медных духовых инструментов Брэкстона оформилась, и ее кульминацией стало выступление в 2007 году в исторической (и достаточно резонансной) церкви Святого Марка в Манхэттен.
Когда я начал работать с Дэйвом Дугласом на Фестивале новой музыки для трубы (FONT), идея организовать концерт с участием медных духовых инструментов Брэкстона оформилась, и ее кульминацией стало выступление в 2007 году в исторической (и достаточно резонансной) церкви Святого Марка в Манхэттен. Композиция полностью использует звуковой потенциал трубы: тембровые сдвиги с несколькими приглушениями; резкие артикуляции, контрастирующие с хриплыми жестами; полуклапанные сжимания и виртуозные пробежки; и звонкие унисоны, гармонии и кластеры, купающиеся в богатых медных обертонах. Даже хореографические движения специфичны для инструмента, не только манипулируя направленностью звука, но и отсылая к вдохновленному Граучо пошатыванию старого товарища Брэкстона Лестера Боуи.
Композиция полностью использует звуковой потенциал трубы: тембровые сдвиги с несколькими приглушениями; резкие артикуляции, контрастирующие с хриплыми жестами; полуклапанные сжимания и виртуозные пробежки; и звонкие унисоны, гармонии и кластеры, купающиеся в богатых медных обертонах. Даже хореографические движения специфичны для инструмента, не только манипулируя направленностью звука, но и отсылая к вдохновленному Граучо пошатыванию старого товарища Брэкстона Лестера Боуи. Однако для меня в этой телесности заключается суть дела; как и большая часть музыки Брэкстона, она требует невозможного, но не требует совершенства, вместо этого волнение заключается в том, что раскрывается в попытке. Медленный распад наших способностей в сочетании с гипнотическим плеском ритмов создает зрелище, подобное огромному тающему леднику, погружающемуся в море. И Энтони был не совсем дружелюбен к нашим амбушюрам. Мы не только открыли пьесу для интермедий групповой импровизации, что позволило людям немного передохнуть, но и статические части пьесы глубоко погрузили исполнителей в педальные регистры в нижней части игрового диапазона их валторн, классическая техника для медных духовых, чтобы освежить свои отбивные. (Хотя на этот раз мы не осмелились попробовать вращающиеся стулья, так что задача для следующего поколения исполнителей остается.)
Однако для меня в этой телесности заключается суть дела; как и большая часть музыки Брэкстона, она требует невозможного, но не требует совершенства, вместо этого волнение заключается в том, что раскрывается в попытке. Медленный распад наших способностей в сочетании с гипнотическим плеском ритмов создает зрелище, подобное огромному тающему леднику, погружающемуся в море. И Энтони был не совсем дружелюбен к нашим амбушюрам. Мы не только открыли пьесу для интермедий групповой импровизации, что позволило людям немного передохнуть, но и статические части пьесы глубоко погрузили исполнителей в педальные регистры в нижней части игрового диапазона их валторн, классическая техника для медных духовых, чтобы освежить свои отбивные. (Хотя на этот раз мы не осмелились попробовать вращающиеся стулья, так что задача для следующего поколения исполнителей остается.) Пристальное внимание к специфике инструментария сочетается с творческим воображением, глобальным и трансидиоматичным. Исполнителям одновременно предлагается продемонстрировать свою техническую виртуозность и импровизационные инстинкты, в то же время им предлагается выйти за пределы предполагаемых способностей и взять на себя захватывающий риск возможной неудачи. Эта музыка помогла мне исследовать новые возможности инструмента, который, как мне казалось, я хорошо знал; независимо от того, хорошо ли вы знакомы с музыкой Брэкстона или слышите ее впервые, я надеюсь, что эта запись вызовет у слушателя такое же чувство открытия. — Тейлор Хо Байнум
Пристальное внимание к специфике инструментария сочетается с творческим воображением, глобальным и трансидиоматичным. Исполнителям одновременно предлагается продемонстрировать свою техническую виртуозность и импровизационные инстинкты, в то же время им предлагается выйти за пределы предполагаемых способностей и взять на себя захватывающий риск возможной неудачи. Эта музыка помогла мне исследовать новые возможности инструмента, который, как мне казалось, я хорошо знал; независимо от того, хорошо ли вы знакомы с музыкой Брэкстона или слышите ее впервые, я надеюсь, что эта запись вызовет у слушателя такое же чувство открытия. — Тейлор Хо Байнум
 Запишите озвучку фильма
Запишите озвучку фильма Не требует регистрации (патч)
Не требует регистрации (патч) 2.1 (2022) PC |.torrent
2.1 (2022) PC |.torrent


 Там же вы можете изменить формат и разрешение.
Там же вы можете изменить формат и разрешение. 


 Clideo — здесь быстро и просто
Clideo — здесь быстро и просто /месяц + бесплатная версия
/месяц + бесплатная версия




 Это делает его одной из бесчисленных популярных потоковых платформ, доступных сегодня.
Это делает его одной из бесчисленных популярных потоковых платформ, доступных сегодня.
 стал одним из самых -посещение российских торрент-сайтов с обширным архивом контента. Доступны многие жанры, от фильмов и сериалов до программного обеспечения и игр.
стал одним из самых -посещение российских торрент-сайтов с обширным архивом контента. Доступны многие жанры, от фильмов и сериалов до программного обеспечения и игр.
 Этот сайт прост в использовании, с отличным интерфейсом и приятным стильным дизайном.
Этот сайт прост в использовании, с отличным интерфейсом и приятным стильным дизайном.

 одно место. На этом сайте есть все: от экшенов до стратегий и даже аниме.
одно место. На этом сайте есть все: от экшенов до стратегий и даже аниме. Годовая подписка на сайт стоит 54 доллара в месяц, если вы платите за год вперед.
Годовая подписка на сайт стоит 54 доллара в месяц, если вы платите за год вперед. Если вы хотите получить доступ к областям, вам нужно будет использовать VPN, чтобы обойти геоблокировку, которую устанавливают эти сайты.
Если вы хотите получить доступ к областям, вам нужно будет использовать VPN, чтобы обойти геоблокировку, которую устанавливают эти сайты. Лучше всего использовать VPN.
Лучше всего использовать VPN. Вот список из 15 активных торрент-сайтов.
Вот список из 15 активных торрент-сайтов.
 torrent-файла в формате JSON
torrent-файла в формате JSON д. С помощью ManageEngine Endpoint Central пользователи могут автоматизировать свои обычные процедуры управления настольными компьютерами, такие как распространение программного обеспечения, установка исправлений, управление ИТ-активами, создание образов и развертывание ОС, и более.
д. С помощью ManageEngine Endpoint Central пользователи могут автоматизировать свои обычные процедуры управления настольными компьютерами, такие как распространение программного обеспечения, установка исправлений, управление ИТ-активами, создание образов и развертывание ОС, и более.
 Может использоваться как подложка для текста
Может использоваться как подложка для текста Нужно,
Нужно, Одним из лучших инструментов для работы является Adobe InDesign, который, к сожалению, довольно трудоемкий. Решение? Создание собственных шаблонов презентаций InDesign.
Одним из лучших инструментов для работы является Adobe InDesign, который, к сожалению, довольно трудоемкий. Решение? Создание собственных шаблонов презентаций InDesign.



 Fohlio — это веб-приложение, которое может автоматически создавать презентации дизайна интерьера во многих форматах, включая файл макета Indesign. Его интеллектуальный плагин для браузера позволяет быстро добавлять информацию о продуктах с любой веб-страницы простым щелчком мыши, а затем упорядочивать продукты по слоям расписания и местоположения. Можно создавать стильные доски настроения с помощью галереи миниатюр и профессиональных презентационных документов. Вы можете обновить их всего за несколько кликов, что отлично подходит для работы на месте.
Fohlio — это веб-приложение, которое может автоматически создавать презентации дизайна интерьера во многих форматах, включая файл макета Indesign. Его интеллектуальный плагин для браузера позволяет быстро добавлять информацию о продуктах с любой веб-страницы простым щелчком мыши, а затем упорядочивать продукты по слоям расписания и местоположения. Можно создавать стильные доски настроения с помощью галереи миниатюр и профессиональных презентационных документов. Вы можете обновить их всего за несколько кликов, что отлично подходит для работы на месте.
 Новичкам этот процесс может показаться сложным и обширным. Тем не менее, техника и среда одинаковы для всех.
Новичкам этот процесс может показаться сложным и обширным. Тем не менее, техника и среда одинаковы для всех. Это поможет присвоить номер каждой доступной странице.
Это поможет присвоить номер каждой доступной странице.
