Математика в ставках на спорт: теория вероятностей. Математика в футболе
Математическое моделирование - Footballworld
Математическая модель и исследование операций
Математика начала применяться еще до того, как стала наукой. Простые арифметические и геометрические понятия и закономерности проникали во все области человеческой деятельности. Попутно с развитием математики расширялся и круг ее приложений. В наше время электронные цифровые вычислительные машины в корне изменили представление о возможностях применения математики. С помощью компьютеров были решены многие ранее поставленные математические задачи прикладного характера.
Прикладная математика призвана создавать, изучать, развивать и совершенствовать методы применения математики к задачам, возникающим за ее пределами. Таким образом, при достаточно широком взгляде на математику прикладная математика является неотъемлемой частью «математики вообще».
Для применения количественных методов исследования в любой области всегда требуется какая-то математическая модель.
Математическая модель - это совокупность математических объектов и соотношений между ними, адекватно отображающая свойства и поведение исследуемого объекта. Математическое моделирование - метод качественного и/или количественного описания процесса с помощью, так называемой математической модели, при построении которой реальный процесс или явление описывается с помощью того или иного адекватного математического аппарата. Математическое моделирование является неотъемлемой частью современного исследования.
При построении модели реальное явление неизбежно упрощается, схематизируется, и эта схема («макет» явления) описывается с помощью того или другого математического аппарата. Чем удачнее будет подобрана математическая модель, чем лучше она будет отражать характерные черты явления, тем успешнее будет исследование и полезнее вытекающие из него рекомендации.
Общих способов построения математических моделей не существует. В каждом конкретном случае модель выбирается исходя из вида операции, ее целевой направленности, с учетом задачи исследования (какие параметры требуется определить и влияние каких факторов отразить). Необходимо также в каждом конкретном случае соразмерять точность и подробность модели:
а) с той точностью, с которой нам нужно знать решение, и
б) с той информацией, которой мы располагаем или можем приобрести.
По форме представления математических моделей различают инвариантную, алгоритмическую, аналитическую и графическую модели объекта проектирования.
В инвариантной форме математическая модель представляется системой уравнений вне связи с методом решения этих уравнений.
В алгоритмической форме соотношения модели связаны с выбранным численным методом решения и записаны в виде алгоритма - последовательности вычислений. Среди алгоритмических моделей выделяют имитационные, модели предназначенные для имитации физических и информационных процессов, протекающих в объекте при его функционировании под воздействием различных факторов внешней среды.
Аналитическая модель представляет собой явные зависимости искомых переменных от заданных величин (обычно зависимости выходных параметров объекта от внутренних и внешних параметров). Такие модели получают на основе физических законов, либо в результате прямого интегрирования исходных дифференциальных уравнений. Аналитические математические модели позволяют легко и просто решать задачи определения оптимальных параметров. Поэтому, если представляется возможность получения модели в таком виде, ее всегда целесообразно реализовать, даже если при этом придется выполнить ряд вспомогательных процедур, Такие модели обычно получают методом планирования эксперимента (вычислительного или физического).
 Графическая (схемная) модель представляется в виде графов, эквивалентных схем, динамических моделей, диаграмм и т.п. Для использования графических моделей должно существовать правило однозначного соответствия условных изображений элементов графической и компонентов инвариантной математических моделей.
Графическая (схемная) модель представляется в виде графов, эквивалентных схем, динамических моделей, диаграмм и т.п. Для использования графических моделей должно существовать правило однозначного соответствия условных изображений элементов графической и компонентов инвариантной математических моделей. К математическим моделям предъявляются требования адекватности, экономичности, универсальности. Эти требования противоречивы.
Важнейшее требование к математической модели состоит в ее адекватности изучаемому реальному объекту, т. е. в правильном описании объекта по соответствующим характеристикам. Так, например, строится математическая модель игры в теннис, адекватная игре по основной характеристике — по изменению счета в гейме (сете). Однако эта модель не учитывает эмоциональных, психологических факторов и адаптации к игре противника. Затем эта модель уточняется и вводится еще одна характеристика — адаптация или обучение в ходе игры. И все же эта модель остается неадекватной реальному процессу по другим особенностям.
Математическая модель должна отражать важнейшие черты явления, все существенные факторы. Вместе с тем, модель должна быть по возможности простой, не «засоренной» массой мелких, второстепенных факторов: их учет усложняет математический анализ и делает труднообозримыми результаты исследования. Как правило, чем модель адекватней реальному процессу, тем она сложней. Поэтому требования простоты и адекватности в определенном смысле противоположны.
Теория игр позволяет найти оптимальные решения или стратегии в математическом моделировании, и ее следует рассматривать не как инструмент предсказания поведения, но как инструмент анализа ситуаций с целью выявления наилучшего поведения для рационального игрока.
Характеристики моделирования распадаются, в первом приближении, на две категории. Одна из них состоит из величин, поддающихся достаточно точному измерению, управлению. Это — детерминированные величины. Другая категория охватывает величины стохастические, имеющие случайную природу и не поддающиеся точным измерениям. Стохастической является модель прогнозирования спортивных результатов. В то же время модель распределения игровых обязанностей в футбольной команде является детерминированной. Такие расчеты могут предоставить совершенно неожиданную и важную информацию. Теория игр имеет значительную познавательную и практическую ценность, ибо позволяет при выборе решения ориентироваться на результаты математического исследования соответствующей игровой модели.
При построении математической модели может быть (в зависимости от вида операции, задач исследования и точности исходных данных) использован математический аппарат различной сложности. В самых простых случаях явление описывается простыми, алгебраическими уравнениями. В более сложных, когда требуется рассмотреть явление в динамике, применяется аппарат дифференциальных уравнений (обыкновенных или с частными производными). В наиболее сложных случаях, когда развитие операции и ее исход зависят от большого числа сложно переплетающихся Идею этого метода можно описать так: процесс развития операции, со всеми сопровождающими его случайностями, как бы «копируется», воспроизводится на машине (ЭВМ). В результате получается один экземпляр («реализация») случайного процесса развития операции со случайным ходом и исходом. Сама по себе одна такая реализация не дает оснований к выбору решения, но, получив множество таких реализаций, мы обрабатываем его как обычный статистический материал (отсюда и термин «статистическое моделирование»), находим средние характеристики процесса и получаем представление о том, как в среднем влияют на них условия задачи и элементы решения.
аналитические, так и статистические модели. Каждый из этих типов имеет свои преимущества и недостатки. Аналитические модели более грубы, учитывают меньшее число факторов, всегда требуют каких-то допущений и упрощений. Зато результаты расчета по ним легче обозримы, отчетливее отражают присущие явлению основные закономерности. А, главное, аналитические модели больше приспособлены для поиска оптимальных решений. Статистические модели, по сравнению с аналитическими, более точны и подробны, не требуют столь грубых допущений, позволяют учесть большое (в теории — неограниченно большое) число факторов. Но и у них — свои недостатки: громоздкость, плохая обозримость, большой расход машинного времени, а главное, крайняя трудность поиска оптимальных решений, которые приходится искать «на ощупь», путем догадок и проб.
Имитационное моделирование применяется к процессам, в ход которых может время от времени вмешиваться человеческая воля. Человек (или группа людей), руководящий операцией, может, в зависимости от сложившейся обстановки, принимать те или другие решения. Затем приводится в действие математическая модель, которая показывает, какое ожидается изменение обстановки в ответ на это решение и к каким последствиям оно приведет спустя некоторое время. Следующее «текущее решение» принимается уже с учетом реальной новой обстановки и т. д. В результате многократного повторения такой процедуры руководитель как бы «набирает опыт», учится на своих и чужих ошибках и постепенно учится принимать правильные решения — если не оптимальные, то почти оптимальные.
Не так уж часто в результате изучения математической модели удается прийти к однозначному решению — найти единственное оптимальное решение. В подавляющем большинстве случаев удается лишь сузить область поиска оптимальных решений (которых может быть несколько), выделить решения, близкие к оптимальным, практически равноценные. Однако и это оказывается успехом, ибо существенно облегчает задачу лица, ответственного за принятие решений, выбрать какое-либо из них.
Применение методов математического моделирования в тренировочном процессе и расчете тактических схем
• Методы математического анализа могут успешно применяться в тренировочном процессе для отслеживания физического состояния игроков, их кондиций и умений, посредством анализа технико-тактических действий каждого игрока во время матча. На основе анализа технико-тактических действий выводится общая оценка игрока за матч. А на основе анализа т/т действий за некоторое количество матче можно вывести примерную (но достаточно адекватную) оценку многих навыков в игре, например: игра головой, действия в отборе, точность паса, точность удара, дриблинг и т.д.
• Имея статистический материал можно более адекватно проводить установку на игру, как отдельным игрокам, так и команде в целом. Математическая модель тактического построения (расстановки игроков на поле и их индивидуальных заданий) позволяет моделировать игровой процесс в игре с соперником. Видеть явные просчеты, слабые места в составе и делать правильные действия, основываясь на бесстрастных математических оценках. Расчеты, конечно, не могут полностью учесть все ньюансы игры, но позволяют с большой долей вероятности предположить характер развития игры. В реальности многое зависит от того, насколько точно игроки выполняют тренерские установки.
• Для команды среднего класса, не имеющей в своем составе звезд мирового класса, наиболее предпочтительна доктрина подбора игроков под избранную тактическую схему. То есть, первична тактика, а игроки подбираются и расставляются на поле, согласно принятой тактической схемы. Для таких команд, одной из наиболее приемлемых тактических схем является тактика 1-4-1-3-2.
• В данной схеме мы имеем: вратаря, правого и левого защитников, двух центральных защитников, опорного хава, трех центральных полузащитников и два нападающих. Центральные защитники играют в линию, но без задания делать искуственный офсайд. Крайние играют на своих бровках до средней линии, лишь изредка переходя на чужую половину поля. Опорный хав играет персонально против плеймейкера соперника. Его основная задача — сорвать организацию атаки соперника. При выполнении стандартов у ворот соперника он занемает одного из центральных защитников, который должен уходить в чужую штрафную для усиления игры на втором этаже. Центральный полузащитник (плеймейкер) является наиболее ответственным звеном в данной расстановке. Он должен быть лидером команды, иметь авторитет у игроков. Обладать хорошим дриблингом, пасом, видением поля. Он выполняет роль свободного художника. Если в составе нет такого игрока, то лучше играть без плеймейкера, так как имеется большая вероятность того, что игра Вашей команды может быть расстроена нейтрализацией одного игрока. Два других полузашитника играют на своих флангах более тяготея к центру. При необходимости место на флангах атаки занимают крайние защитники. При выборе пары нападающих необходимо обратить внимание на следующее. В идеале пара нападающих должна состоять из тяжелого (таранного типа, хорошо играющего головой) и легкого (быстрого, с дриблингом и ударом). Данная схема не претендует на безоговорочную истину, но методами математического моделирования она дает хорошие результаты в играх с соперниками разного класа, имея в своем составе средних игроков. Это только короткое, эскизное описание схемы.
• Математический аппарат, применяемый в тренировочном процессе, пока еще не достаточно развит. И большая часть разработок в этом направлении являются собственностью клубов, их коммерческой тайной, ноу-хау. Ярким примером является «Бавария», большинство английских клубов всех лиг, некоторые норвежские и шведские клубы. Как правило, клубы, имеющие математические модели, видно сразу.
sites.google.com
Математика и теория вероятности в ставках на спорт 2018
Математика в ставках имеет решающее значение. На этой точной науке построен весь букмекерский бизнес. Нельзя получить прибыль, надеясь лишь на свои догадки, внутреннее чутьё. Понимание этой концепции отличает победителя от неудачника, успешного игрока от минусового, который регулярно проигрывает свои сбережения в букмекерской конторе. Большинство любителей спортивных пари теряют деньги, а ведь совсем не сложно выделить немного времени и разобраться с основными математическими понятиями в ставках на спорт. Если хотите влиться в ряды плюсовых беттеров, получив знания о том, как работает математика в спортивных ставках, то данная статья поможет вам в этом.

Быстрый переход
Теория вероятностей
Начнём разбор этой интересной темы с общих понятий. Первый вопрос, который имеет отношение к теории вероятностей – букмекерские коэффициенты. Эти числа должны отражать вероятность того или иного события: победы, тотала, форы. Как рассчитать вероятность с помощью букмекерского коэффициента? Очень просто, нужно разделить единицу на выставленный коэффициент:

Для примера возьмём матч английской Премьер-лиги между Арсеналом и Манчестер Юнайтед. Букмекер выставил следующие котировки на этот поединок: победа Арсенала 2,05; ничья 3,60; победа МЮ – 3,80. Производим поиск вероятностей всех трёх событий и получаем: виктория Арсенала вероятна на 49%, вничью команды сыграют с вероятностью 28%, Манчестер имеет лишь 26% шансов на успех. В идеале эта сумма должна составлять 100%, но сложив все три числа, получим 103%. Лишние в данном случае 3% — это процент букмекера, или маржа, которую он берёт за свои услуги. 3 процента — это маленькая маржа. Букмекер делает её такой, чтобы завлечь больший поток ставок на топовые встречи. На менее популярные матчи и у более «скупых» контор маржа может достигать 8 процентов и более. Отняв процент маржи, получим истинное значение: 48% — 27% — 25%. Пересчитав полученные данные в коэффициенты при помощи обратной формулы, видим: 2,08 – 3,70 – 4.

Некоторые люди утверждают, что нельзя получить прибыль посредством ставок, так как весь профит уйдёт на маржу. Но это было бы верно в том случае, если бы букмекерские коэффициенты были реальным отражением вероятности события. К счастью для беттеров, никто не может со стопроцентной точность предсказать исход будущего поединка, даже букмекер. Тем более конторы допускают ошибки сознательно, уменьшая маржу на «громких» матчах, а в непопулярных чемпионатах выставляют котировки, исходя только из статистики и не учитывая других важных факторов, которые влияют на мотивацию и саму игру. Такие недооценённые ставки называются валуйными (от англ. Value bet – ценная ставка). Успешный поиск валуйных пари и есть целью для преуспевающего игрока.
Как же математика в спортивных ставках поможет определить, является ли ваш выбор ценным? Это второй вопрос, имеющий отношение к теории вероятностей. Для этого нужно оценить собственную вероятность события. В качестве примера рассмотрим поединок испанской Ла Лиги Леганес – Бетис. Коэффициент на победу хозяев 1,65; ничья котируется за 3,8; на гостей можно поставить за 6,3. Проводим предматчевый анализ, и получаем следующие вероятности: победа Леганеса 45%, ничья 25%, победа Бетиса 30%. Рассчитаем валуйность для каждого выбора:
П1: 1.65*0.45-1=-0.2575
Х: 3.8*0.25-1=-0.05
П2: 6.3*0.3-1=0.89
Как видно, букмекер недооценил возможную победу гостей, и котировка на этот исход является валуйной.

Третий вопрос, даже догма, которую должен усвоить любой клиент букмекерской конторы – финансовая математика. В качестве опыта возьмём монету и будем подбрасывать её, фиксируя результаты. Очевидно, что при идеальных условиях вероятность, или другими словами математическое ожидание, выпадения орла или решки составляет 50 процентов. Но при малом количестве испытаний результаты могут кардинально отличаться от ожидаемых. Если подбросить монету десять раз, то возможен и такой вариант, что во всех десяти опытах выпадет решка. Такое неравномерное распределение называется дисперсией. При ста испытаниях такое уже невозможно, количество выпавших решек будет в пределах от 40 до 60. Если осуществить 1000 бросков, дисперсия сгладится ещё больше – получим от 440 до 560 решек. Для получения 50 процентов решек необходимо провести бесконечное количество опытов.

Причём здесь финансовая математика и в чём ценность этого примера для беттера? Всё дело в дисперсии. Именно эта коварная закономерность может легко уничтожить игровой банк при неправильном менеджменте и выделении слишком большой суммы на одну ставку. Неудачная полоса даже из пяти минусов в ряд обнулит ваш аккаунт, если позволять себе заключать одно пари на 20 процентов от банкролла. Поэтому крайне важно рисковать не более 1-2% на отдельно взятой ставке. Также необходимо уяснить, что ставки – это долгосрочная инвестиция, а не быстрый заработок. При малом количестве заключенных сделок из-за дисперсии даже опытный и успешный беттер может оказаться в минусе, а новичок поймать серию побед и возомнить себя гуру в беттинге. Но только дистанция покажет кто есть кто. Прояснить ситуацию о ваших способностях в этой сфере поможет выборка в 500, а лучше в 1000 ставок.
Метод Монте-Карло
Математика в ставках проявляется не только в поиске ценных предложений. Есть также некоторые вспомогательные способы, позволяющие увеличить шансы на успех. Первый из них – метод Монте-Карло, разработанный в прошлом веке Станиславом Уламом. Принцип данной методики – получение множества результатов, которые напрямую зависят от исходных данных. Любой входной параметр, который не может быть установлен точно, представлен в виде большого количества вариантов. После обработки в результате получим набор всех возможных исходов с соответствующими им вероятностями.

Для большей ясности в качестве иллюстрации возьмём гипотетическую ситуацию в чемпионате Испании по футболу, где за чемпионство сражаются Барселона, Реал и Валенсия. До конца первенства 7 туров, клуб из Барселоны является лидером, валенсийцы вторые, мадридцы занимают третье место. Требуется узнать, каковы шансы Валенсии на золотые медали. Снова нам поможет математика в ставках на спорт. Метод Монте-Карло позволит скомпилировать все возможные результаты за оставшиеся туры. Чем качественнее и обширнее входные данные – сведенья о форме команд, индивидуальном мастерстве исполнителей, травмах ключевых игроков и так далее, тем точнее будет результат. Все параметры можно записать в форме пропорций. Допустим, ситуацию с составами и травмами можно выразить как 1:2:3. То есть первая команда играет оптимальным набором игроков и ей отдаётся преимущество, а третья значительно пострадала от различных повреждений. Сгенерировав все, возможные варианты, узнаем примерные шансы валенсийцев на первое место.
Цепь Маркова
Второй инструмент, на основе которого строится математика в спортивных ставках – цепь Маркова. Этот подход гласит, что вероятность будущего зависит только от того, что есть в данный момент, прошлое никак не может повлиять на возможный исход. Если сказать словами из мира беттинга, то это значит, что любой матч индивидуален. И? к примеру, результат нынешней встречи Спартак – Зенит совершенно не будет зависеть от тех поединков, которые команды сыграли два или три года назад. Необходимо учитывать только текущее положение дел – форму, мотивацию, составы, погоду и так далее. Для анализа важны лишь поединки команд за последние две-три недели или календарный месяц. Финансовая математика игрока будет показывать только тенденцию к росту банка, если грамотно внедрить систему Маркова.

Байесовская вероятность
Два столетия назад Томом Байесом была разработана теория, которая имеет актуальность для беттеров и по сей день. Байесовский принцип гласит: новые обстоятельства влияют на вероятность того или иного исхода. Его можно записать в виде формулы:
 где:
где:
P(X/Y) – вероятность события Х при условии Y;
P(X) – вероятность события Х;
P(Y/X) – вероятность события Y при условии события Х;
P(Y) – вероятность события Y.

К примеру, интересно ли вам, как погода влияет на коэффициенты на поединок с участием любимого клуба? Снова нам поможет математика в ставках, а именно созданная Байесом теория. Букмекер оценивает шансы на победу ваших любимцев с вероятностью 60%. В 20% победных встреч вашей команды шёл дождь, а средняя вероятность осадков во время поединков 25%. Проведём расчет:
P(X/Y)=(60*25)/20=75%
То есть, вероятность победы ваших любимцев в дождливую погоду составляет 75 процентов.

Математика в ставках, и в частности финансовая математика, являются основой беттинга, и об этом нужно помнить всегда, даже если у вас затянувшаяся чёрная полоса. Знайте – дистанция сгладит дисперсию, и на первое место выйдет ваше мастерство. А увеличить шансы на успех помогут метод Монте-Карло, цепь Маркова и Байесовская вероятность.
Трекбэк с Вашего сайта.
rushbet.ru
Исследовательская работа по математике Математика и спорт
МБОУ Щенниковская основная школа
Районная научно-практическая конференция
«ПЛАНЕТА ОТКРЫТИЙ»
Секция: МАТЕМАТИКА
Тема работы: «Математика и спорт. Есть ли связь между ними?»
Автор: Иванов Денис
Класс: 6 класс
Руководитель: Пирожкова Валентина
Васильевна, учитель математики
село Щенники
ОГЛАВЛЕНИЕ
Введение…………………………………………………………………….2
Глава 1. Математика и спорт, есть ли связь между ними?.....................5
Как применяется математика в футболе…………………… …7
Как применяется математика в волейболе……………………..9
Как применяется математика в лыжных гонках……………….11
Глава 2. Анкетирование обучающихся и их родителей по теме «Твое отношение к спорту», обработка результатов анкетирования……………..15
Заключение………………………………………………………………....19
Список литературы…………………………………………………………20
Приложения ………………………………………………………………...21
ВВЕДЕНИЕ
Я с детства занимаюсь спортом. Ещё когда ходил в детский сад, всё своё свободное время я проводил на спортивной площадке: летом – играл в футбол, зимой – гонял на лыжах. Потом, когда стал учиться в школе, моя любовь к спорту не прошла, а только усиливалась – сначала я стал посещать секцию по футболу в ДЮСШ, а сейчас занимаюсь в ФОКе и уже имею различные награды.
Но всё-таки основным видом моей деятельности является учёба. Среди всех школьных предметов мне больше всего нравится заниматься математикой. И когда учитель предложил мне принять участие в районной конференции «Планета открытий», я решил взять тему «Математика и спорт. Есть ли связь между ними?» чтобы разобраться, присутствует ли математика в спорте и насколько это важно. Я считаю, что эта тема актуальна, так как в современном мире интернета, телефонов, компьютеров и других «умных» устройств многие дети перестают не только заниматься спортом, но и редко выходят на прогулки с друзьями, предпочитая просиживать всё свободное время в интернете. А ведь чтобы создать всю эту технику – без математики не обойтись!
Исходя из вышеперечисленного, я поставил для себя цель: выяснить взаимосвязь математики и спорта.
Для достижения поставленной цели необходимо решить следующие задачи:
Изучить литературу о взаимосвязи математики и спорта;
Привести примеры применения математики в различных видах спорта;
Оформить полученные данные с помощью наглядной интерпретации информации;
Проанализировать анкеты учеников и их родителей.
Чтобы попытаться решить проблему я выдвинул следующую гипотезу: чтобы достичь высоких результатов в каком-либо виде спорта, нужно правильно применять математические знания.
В работе использовались следующие методы исследования:
изучение литературы;
использование интернет-ресурса при изучении вопроса;
анализ и синтез;
анкетирование;
обобщение собранного материала;
защита исследовательской работы.
Объект исследования: математика.
Предмет исследования: область математика и спорт.
Исследовательская работа проводилась в течение двух месяцев (февраль, март). На первом этапе мною был изучен материал печатных изданий и интернет-ресурсы, затем я выбрал наиболее интересующие меня виды спорта, о которых будет рассказано в работе (футбол, волейбол, лыжные гонки). После этого я провёл анкетирование учеников и их родителей и проанализировал полученные данные.
Глава 1. Математика и спорт, есть ли связь между ними?
Помните, ум – ваш лучший
мускул.
Сильвестр Сталлоне.
Ни для кого не секрет, что занятие спортом благотворно влияют на умственную деятельность и психику человека, укрепляют его волю. Этот факт бесспорен для многих ученых, занимающихся плаванием, теннисом, бегом, лыжами, альпинизмом. Следует назвать многих крупных ученых — Б. Понтекорво, Дж. Литлвуда, Р. Пэли — сочетавших науку со спортом. Нильс Бор и Харольд Бор играли в классной футбольной команде, Нильс Бор был отличным лыжником, Альберт Эйнштейн увлекался вождением яхт.
Математические методы все шире используются в спорте. Трудно себе представить, сколько еще нерешенных проблем возникает при рассмотрении взаимодействия мяча и ракетки, мяча с грунтом или травой.
Перечислим типичные задачи, которые могут быть рассмотрены методами теории исследования операций.
- Распределение игровых амплуа в спортивной команде (баскетбольной, хоккейной и др.), обеспечивающее наибольший эффект в игре.
- Системы организации чемпионатов, турниров и кубковых встреч (шахматных, теннисных, хоккейных и др.), обеспечивающие достижение определенных целей. Например, для: выявления первого и второго призеров кубковой встречи (с соблюдением определенных условий). Или, например, для того чтобы в матче двух шахматных команд обеспечить следующие естественные условия:
а) все участники играют одинаковое число партий фигурами каждого цвета;
б) в каждом туре участники обеих команд играют одинаковое число партий белыми и черными;
- Составление для спортсменов диеты, удовлетворяющей требованиям медиков и, в то же время, наиболее экономной и сохраняющей вес спортсмена в определенных рамках, а также подборка содержимого рюкзака с продуктами, обеспечивающая при наименьшем его весе необходимый рацион.
Математика – это наука, которая изучает величины, количественные отношения и пространственные формы. Математика царица всех наук. Математика невозможна без цифр. Мы повсюду видим использование натуральных чисел в любых видах спорта. В каждом соревновании ведется счет на время. Без счёта нет и игры. В математике жизнь спорта. Давайте рассмотрим некоторые примеры:
Любой вид соревнований на скорость (бег, плавание, автогонки и др.)подразумевают подсчет результата в часах, минутах, секундах, а время у нас записывается ЦИФРАМИ! Разница между результатами - это простейшие арифметические действия! В игровых видах спорта (футбол, баскетбол, теннис, водное поло и др.) счет идет на очки. А очки это тоже ЦИФРЫ! Разница между очками есть математическое вычисление. В таких видах спорта как гимнастика, фигурное катание, прыжки в воду подсчет результата ведется с помощью баллов. Баллы даются судьями за выполнение того или другого элемента. И опять кто набрал больше баллов, помогает определить математика!
Немало интересных закономерностей математики обнаружили в спорте. В числе прочего они объяснили, почему левши имеют преимущество при игре в бейсбол, вывели связь между длиной пятки и спринтерскими качествами спортсмена, определили идеальную форму шара для гольфа и разработали наиболее эффективную тактику удара клюшкой. В атлетике крайне важны арифметические расчеты при разбеге прыгуна в длину для максимально четкого попадания «шиповкой» на планку отталкивания. Так же крайне важным арифметическим попаданием является степень упругости шеста у прыгунов в высоту.
Я решил рассмотреть, как применяется математика в футболе, волейболе и лыжных гонках.
Как применяется математика в футболе
Футбол – самая популярная спортивная игра в мире. Математика имеет самое непосредственное отношение к этому виду спорта. Взять даже самые азы математики – счет. Не умей считать, человек не смог бы подсчитать голы команд, а без этого футбола быть не может. Математика присутствует в самых различных компонентах этой интереснейшей игры – начиная от конструкции футбольного мяча, и заканчивая спортивными рейтингами. 
Всем нам знакомый черно-белый футбольный мяч представляет собой геометрическую фигуру – икосаэдр. Икосаэдр – это правильный выпуклый многогранник. В данном случае икосаэдр состоит из 20 шестиугольных и 12 пятиугольных граней. Круглым он становится, когда его наполняют воздухом. 
Ширина ворот (находящихся по середине лицевой линии) равна 7,32 м., а высота – 2,44 м(отношение 3/1). Сетка ворот различается формой ячеек, они могут быть в форме квадрата, шестигранника и ромба. Ширина линии ворот равна диаметру стоек и перекладины. Ворота условно делятся на девять квадратов: три ряда по три квадрата. Каждому квадрату присваивается номер от 1 до 9. Счёт начинается с нижнего ряда, так что над первым квадратом располагается четвёртый, над четвёртым—седьмой, и т. д.
Поле делится на две абсолютно симметричные части. Центральный круг имеет радиус 9,15 м. Такой же радиус имеет полукруг штрафной площади с центром в 11-метровой точке. Ширину штрафной площади можно разделить на три равные 5,5 м отрезка, концами которых будут линия вратарской, конец вратарской площади, 11-метровая точка и конец штрафной площади. 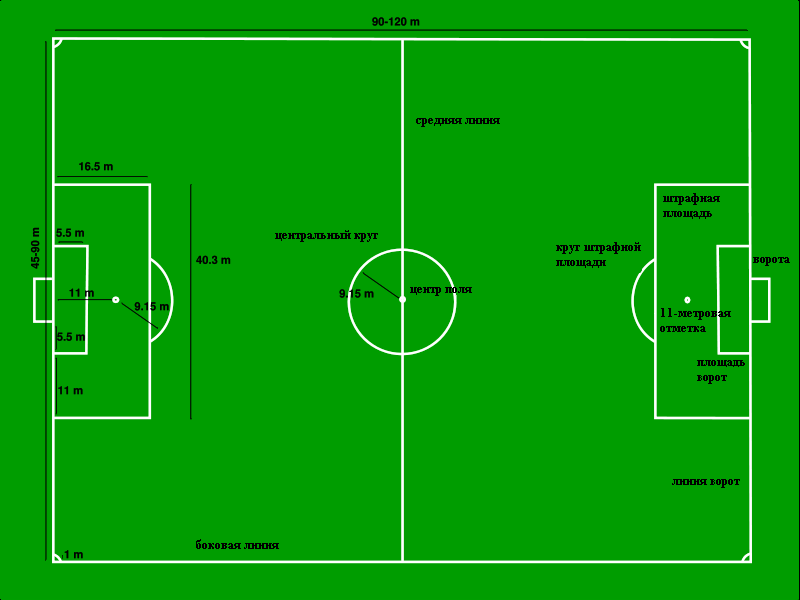
При подготовке команд и их тренеров к серьезной схватке с соперниками все математические методы работают как никогда. Например, определение оптимального состава на игру в футбольном матче, оптимальной расстановки игроков на футбольной поле, в том числе – учет командного взаимодействия и много другое – невозможно без применения математики. Удалось доказать, что оптимальная стратегия в выигрыше чемпионата по футболу может включать и такой вариант, как поражение в отдельных матчах. Такая ситуация может возникать, когда команда, уже обеспечившая себе место в высшей лиге, должна провести еще одну встречу в своей (низшей) лиге. Однако, в случае победы ей пришлось бы в первом туре высшей лиги встретиться с весьма сильным противником, в случае проигрыша — с более слабым. Анализ ситуаций позволяет выдать рекомендации о том, когда следует стремиться к победе, а когда смириться с поражением.
Таким образом всеми вышеизложенными примерами я доказал , что без математики футбол немыслим. Начиная от дворового футбола, где игроков интересует только счет и заканчивая профессиональными футбольными клубами, с их сложными расчетами, тактическими схемами, бухгалтерским балансом и прочими математическими вкладками, я наблюдал активное применение математики в этом виде спорта.
1.2. Как применяется математика в волейболе
Волейбол – одна из самых популярных спортивных командных игр. Играют в волейбол две команды по шесть человек, на ровной площадке оговоренных размеров, разделенной посередине сетью, верхний край которой должен быть закреплен на высоте 243 см для мужчин и 224 см для женщин. Правила классического волейбола таковы: Каждая из двух команд может иметь в составе до 14 игроков, на поле во время игры могут находиться 6 игроков. Игра состоит из пяти отрезков (партий), первые четыре из которых играются до достижения какой-либо командой 25-и очков, а финальная – до 15-и. Мяча разрешено касаться любой частью тела. Для достижения хороших результатов на серьезных соревнованиях необходима не только хорошая сыгранность всей команды, но и специфические требования: ловкость, прыгучесть, развитая мускулатура рук, без которой не нанесешь сильного удара по мячу. Кроме того, спортсменам-волейболистам необходимо иметь высокий рост, чтобы им было легче выпрыгивать над сеткой. В командах-участницах международных состязаний, большинство игроков выше 200 см.
Волейбольная партия не ограничена во времени и продолжается до 25 очков, в пятой партии (тай-брейк) счёт идёт до 15 очков. При этом если преимущество над противником не достигло 2 очков, партия будет продолжаться до тех пор, пока это не произойдёт.
В каждой партии тренер каждой из команд может попросить два тайм-аута по 30 секунд. Дополнительно в первых 4 партиях назначаются технические тайм-ауты по достижении одной из команд 8 и 16 очков (по 60 секунд).
Волейбольный мяч состоит из шести панелей кожи (естественной или искусственной), натянутой вокруг каркаса. Каждая панель состоит из трёх секций или рядов. Мяч может быть разноцветным или полностью белым. Длина окружности мяча 65—67 см; вес — 260—280 г. Внутреннее давление 0,300 — 0,325 кг/см2 (294,3—318,82 гПа).
Волейбольная площадка — ровная и строго горизонтальная площадь прямоугольной формы, ограниченная разметкой, являющаяся местом проведения волейбольных матчей.
Размер площадки в длину 18 метров и 9 метров в ширину. Площадка разделена на две части размером 9×9 метров с помощью сетки метровой ширины. Сетка расположена таким образом, что её высшая точка находится на высоте 2,43 метра от земли на мужских соревнованиях и 2,24 метра — на женских (высота может изменяться для соревнований ветеранов и юниоров). С двух сторон сетка ограничена двумя вертикальными антеннами, которые являются продолжением боковой линии площадки и определяют разрешённое правилами пространство игры мячом.
Параллельно сетке на расстоянии трёх метров с каждой стороны от неё проводятся линии, называемые линиями атаки.
Площадка окружена свободным пространством (так называемая свободная зона), имеющим сбоку не менее 3 метров, спереди - сзади не менее 5 метров и по высоте не менее 7 метров, на официальных соревнованиях FIVB. Игроки могут входить в свободную зону и играть в её пределах после подачи мяча.
1.3. Как применяется математика в лыжных гонках
Лыжный спорт и математика между ними огромная и непосредственная связь, потому что когда человек бежит на лыжах у него мобилизуются все системы органов, у него хорошо работает дыхательная система, сердечная система, мышечная система, в результате чего у него лучше начинают работать мозги. Улучшаются и ускоряются все нервные процессы, поэтому, чем человек чаще встает на лыжню, тем лучше повышается его интеллект, который необходим на занятиях математикой.
Я люблю заниматься лыжными гонками и у меня уже есть определённые успехи в этом виде спорта: 3 место в районных соревнованиях «Лыжня России – 2016», 2 место в соревнованиях «Щенниковская лыжня – 2016».
Лыжные гонки – это вид лыжного спорта, в котором участникам – спортсменам необходимо преодолеть соревновательную дистанцию на лыжах, при этом обогнав своих соперников. Грамотная техника передвижения на лыжах представляет систему движений, при помощи которой спортсмен может добиться максимальной эффективности своих действий. Существует два основных стиля передвижения на лыжах – коньковый (свободный) и классический. К классическому стилю относят виды передвижения, в процессе которых лыжник проходит практически всю предназначенную дистанцию по заранее подготовленной лыжне, которая состоит из двух колей, расположенных параллельно друг другу. Стоит отметить, что классический ход существенно уступает свободному в скорости. 
Кроме того, нужно правильно выбрать беговые лыжи и палки к ним.
лыжника(см)Длина лыж дляклассического хода(см)
Длина лыж для прогулок(см)
Длина лыж дляконькового хода(см)
150
170-180
165-170
165
155
175-185
170-175
170
160
180-190
175-185
175
165
185-190
180-185
180
170
190-195
185-190
185
175
195-200
190-195
185
180
195-200
195-200
190
185
200-205
200-205
190-195
190
205-210
205-210
195-200
195
205-210
205-210
200-205
Беговые лыжи.Длина. Есть два способа выбора длины лыж. Основные – это либо вытянуть руку вверх и из получившейся высоты отнять 10 см, либо к собственному росту прибавить 10-15 см. Кроме того, есть специальные таблицы, по которым можно точнее вычислить длину лыж (из неё видно, что возраст и вес имеет значение при выборе). Вот одна из них:
Жёсткость. Жёсткость лыж проще всего проверить таким образом. Нужно положить лыжи на пол и встать на них. Второй человек в это время берёт лист бумаги и проводит им между лыжей и полом вперёд и назад под ботинком, тем самым проверяя расстояние – в идеале оно должно быть 30-45 см вперёд и 10 см назад. Затем надо перенести вес тела на одну лыж и сделать всё то же самое, в этом случае зазор не должен быть больше 10 см с одной и другой стороны. Если зазор больше, то лыжи слишком жёсткие, если же меньше – соответственно, слишком мягкие. Для ребёнка нужно брать лыжи помягче. На них ему будет проще учиться кататься. Кроме того, ни в коем случае нельзя брать детям лыжи длиннее положенного – так часто делают, считая, что сэкономили, и ребенок несколько лет будет кататься на них. В этом состоит ошибка – такие лыжи не будут «слушаться» ребенка, и, возможно, это отобьёт всякое желание пробовать дальше. Это касается и лыжных палок, которые тоже не надо брать «на вырост». Лыжные палки. Длина лыжных палок для классического стиля катания должна быть на 25-30 см меньше роста лыжника. Длина лыжных палок для конькового стиля катания должна быть на 15-20 см меньше роста лыжника.
Строго фиксируются время старта и время финиша спортсмена. Много можно выиграть на поворотах, если бежать по меньшему радиусу. Например, если трасса имеет девять поворотов и на каждом пройти по меньшему радиусу, сэкономив на каждом повороте по пять секунд, то на всей дистанции сэкономишь 45 секунд. Каждый лыжник на дистанции распределяет свои силы в процентном соотношении своей максимальной скорости.Таким образом, техника лыж - это сплошная физика, которая вычисляется с помощью математических расчётов. Знание физики и математики позволит лыжнику – спортсмену добиться более высоких результатов, а любителю почувствовать всю прелесть лыжной гонки.Я рассмотрел только три вида спорта и увидел, что в них невозможно обойтись без математики. Математика присутствует в спорте повсюду и даже в самых элементарных подсчетах, которые требуются для выявления победителей.
Большой спорт - это математика. Сначала нужно тренировать мозг, а потом - ноги и руки.
Глава 2. Анкетирование учащихся и их родителей по теме «Твое отношение к спорту», обработка результатов анкетирования.
Работая над темой, я провел опрос среди учащихся нашей школы и их родителей на предмет их отношения к спорту и математике.
Результаты анкетирования учащихся
В анкетировании участвовали 14 учащихся 4-8 классов нашей школы.
На первый вопрос анкеты «Занимаешься ли ты спортом?» получены следующие результаты: да – 11 чел., нет – 2 чел., иногда – 1 чел.
На второй вопрос «Ты занимаешься один или вместе с родителями?» из тех ребят, что занимаются спортом, ответили так: один – 10 чел., иногда с родителями – 1 чел.
Видно, что родители практически не занимаются с детьми спортом, а жаль.
На третий вопрос «Какие виды спорта тебе больше нравятся?» были получены такие ответы: футбол – 7 чел., гимнастика – 3 чел., бег – 2 чел., лыжные гонки – 2 чел., теннис – 2 чел., волейбол – 2 чел.
Как видно из диаграммы, большинству ребят нравится заниматься футболом, гимнастикой. Некоторые предпочитают бег, теннис, лыжные гонки, волейбол. Но в нашем селе нет возможности заниматься гимнастикой, теннисом. Играть в футбол и волейбол дети могут только летом в сухую погоду на спортивной площадке.
На четвёртый вопрос «Почему нужно заниматься спортом?» ученики ответили так: чтобы быть здоровым – 12 чел., чтобы быть сильным – 2 чел.
Как видно из диаграммы у большинства учеников желание заниматься спортом сугубо личное - собственное здоровье. Спорт для них – это не только престиж, но и, что самое важное, способ укреплять свое здоровье.
На пятый вопрос «Нравятся ли тебе уроки математики?» ответили таким образом: да – 8 чел., нет – 3 чел., не всегда – 3 чел.
На шестой вопрос «Есть ли связь между математикой и спортом?» ученики дали такие ответы: да – 9 чел., нет – 4 чел., не знаю – 1 чел.
Доказано, что те дети, которые регулярно занимаются спортом, ведут активный образ жизни, избегают вредных привычек, показывают лучшие результаты и в учебе. Полученные результаты анкетирования подтверждают, что математика и спорт тесно связаны друг с другом.
На седьмой вопрос «Хотел бы ты достичь успехов в занятиях спортом?» были даны следующие ответы: да – 11 чел., нет – 2 чел., не знаю – 1 чел.
Видно, что в основном, ребята хотят добиться успехов в занятиях спортом, но для этого нужно приложить максимум усилий.
Результаты анкетирования родителей
В анкетировании приняли участие 9 родителей учащихся. Результаты получились следующие:
Н
На первый вопрос «Являетесь ли Вы примером для своего ребёнка в занятиях спортом?» ответили: да – 2 чел., нет – 6 чел., не знаю – 1 чел. Видно, что большинство родителей не являются примером для своих детей в занятиях спортом.
На второй вопрос «Считаете ли Вы занятия спортом важными и нужными в жизни ребёнка?» получены такие результаты: да – 7 чел., нет – 2 чел.
На третий вопрос «Поддерживаете ли Вы спортивные увлечения своего ребёнка?» я получил такие ответы: да – 6 чел., нет – 3 чел.
На четвёртый вопрос «Какие спортивные традиции существуют в Вашей семье?» ответили так: никакие – 5 чел., кататься на лыжах – 2 чел., тур. поход – 1 чел., труд – 1 чел. Можно сделать вывод, что в семьях практически не поддерживаются никакие спортивные традиции, что очень плохо отражается на детях, которые стремятся заниматься спортом.
На пятый вопрос «Как Вы считаете, есть ли связь между математикой и спортом?» получены такие ответы: да – 8 чел., нет – 1 чел.
На шестой вопрос «Если да, то в чём она заключается?» ответили так: в счёте – 5 чел., в скорости – 3 чел., длина дистанции – 1 чел.
На седьмой вопрос «Воспитываете ли Вы своего ребёнка на уважении к людям, которые приносят славу стране спортивными достижениями?» были даны такие ответы: да – 8 чел., нет – 1 чел. Можно сказать, что большинство родителей хотят, чтобы их дети гордились достижениями наших спортсменов, брали с них пример.
Проанализировав ответы детей и их родителей можно сделать такой не утешительный вывод: если в детском и подростковом возрасте ребята в большинстве занимаются каким-либо спортом, то становясь взрослыми, это увлечение у большинства людей проходит.
ЗАКЛЮЧЕНИЕ
«Математика – царица наук!» Всем нам хорошо известно это высказывание. И, действительно, проводя исследовательскую работу, я увидел, что даже спорт не обходится без знаний математики. Я открыл для себя, что математика используется в спорте не только для подсчёта очков. В современном спорте довольно широко используется математический аппарат – анализируются графики различных зависимостей, выводятся математические формулы, проводится математическая обработка данных. Таким образом, можно сказать, что математика — очень важный предмет в спорте.
Исходя из проделанной работы, я сделал следующие выводы:
- Ни один вид спорта не обходитcя без математики.
-Спорт это интеллектуальный род занятий, практическая математика помогает добиваться высоких спортивных результатов.
- Наша гипотеза подтвердилась: чтобы достичь высоких результатов в каком-либо виде спорта, нужно правильно применять математические знания.
СПИСОК ЛИТЕРАТУРЫ
Математика и спорт, Садовский Л.Е., Садовский А.Л., М. «Наука», 1985.
http://www.kakprosto.ru/kak-243697-chto-takoe-voleybol#ixzz43cxfVLAd
SportSchools.ru
http://mirsovetov.ru/a/sorts/sports-ware/choose-skis.html
ru.wikipedia.org
http/index.php/biblioteka/matematika/1921-matematika_i_sport 12.
https://yandex.ru/images/search?img_url=http%3A%2F%2F
https://yandex.ru/images/search?text=игра%20в%20волейбол
https://yandex.ru/images/search?text=лыжные%20гонки
http://www.sportzone.ru/
http://www.math.ru/lib/bmkvant/44
http://nashol.com/2012041764632/matematika-i-sport-sadovskii-l-e-sadovskii-a-l-1985.html
ПРИЛОЖЕНИЯ


Анкетирование учащихся по теме «Твое отношение к спорту»


Анкетирование родителей по теме «Твое отношение к спорту»








Мои спортивные достижения
infourok.ru
Математика в ставках на спорт. Расчет и алгоритмы
Для игрока думающего, который желает делать прибыльные ставки, математика может оказать неоценимую услугу в плане не только подбора стратегии, но и вычисления нормальной букмекерской конторы, которая ставит минимальную маржу, а значит, позволяет игроку играть с плюсовым балансом ставок.

Содержание страницы
Математический расчет ставок на спорт
Пример №1. Вычисление маржи букмекера
Не секрет что многие букмекеры жадничают, когда выставляют в линии коэффициенты. Для подбора нормального гемблинг-оператора, который забирает себе минимальный процент со ставки и дает высокие коэффициенты, достаточно научиться самому считать маржу конторы. Вот простой пример: футбольный матч Спартак — Анжи. Букмекер в линии предлагает коэффициенты: П1-1.29, Х – 4.75, П2 – 9.00. Путем простейших вычислений считаем какую маржу оператор заложил на этот матч по формуле М = (1/Кф1 +1/Кфн + 1/Кф2) – 1, М – маржа, Кф1 – коэффициент на 1 команду, Кфн – коэффициент на ничью и Кф2 – коэффициент на 2 команду.
(1/1.29 +1/4.75+1/9.00) – 1 = (0.77+0.21+0.11) – 1 = 0.09, это означает, что букмекер заложил маржу на этот матч в размере 9%. Такой процент маржи указывает сразу, что ставить в этом гемблинг-операторе длительный период свои ставки — бесперспективно. Контора с нормальным потолком маржи не превысит ее более чем 5%, это важный фактор.
Пример №2. Выбор правильной математической стратегии
Для математического расчета ставок на спорт придуманы различные стратегии ставок. Их немало, таких стратегий — Флэй, Мартингейл, Датская система, принцип Д’аламбера, Фиксированная ставка, Валлей беттинг – все они основаны на математических расчетах, которые призваны минимизировать потери игрока при сделанных неудачных ставках. Стратегии эти можно подобрать с помощью нашего сайта, который детально расписывает, как ими ставить и какие особенности каждая из них имеет.
Каждая из стратегий имеет свой математический расчет, формулу и детальные пояснения как он работают и как играть, так что пренебрегать ими не стоит.
Пример №3. Математические ставки на спорт: вероятность при расчете
Еще одной математической составляющей теории беттинга является математическая вероятность. Этот фактор нужен бетторам, которые хотят играть длительный период игры и делать свои ставки абсолютно обдуманно, используя математические алгоритмы ставок на спорт.
Вот какая формула математической вероятности:
МВ = (СС * К — СС) * П – СС * Ф
Обозначения:
СС – сумма ставки.К – коэффициент ставки.П – победа (ее вероятность).Ф – фиаско (поражение).СС * К – СС – размер выигрыша.

МВ – математическая вероятность.

Математическая вероятность позволит оценить выгоду от своих ставок в долгосрочной беттинг-перспективе, рассчитано оно на большое количество всех ставок.
Основной показатель: если математическая вероятность больше 0, то беттор будет в плюсе, цифры меньше 0 сулят проигрыш.
Рассмотрим элементарный пример футбольного матча Спартак — Локомотив, команды приблизительно равны по силам, небольшое преимущество есть у Спартака в случае более стабильной игры и лучших результатов.
Беттор оценивает все факторы и принимает вероятность выигрыша Спартака 65% (0.65) — Локомотив — 35% (0.35).
Конторы дают коэффициенты на данный матч: Спартак – 1.68, Локомотив — 2.05.Ставит беттор на Спартак 100 €, рассчитывает, таким образом, свою вероятность выигрыша:
МО = (100 * 1.68 — 100) * 0.65 – 100 * 0.35МО = 9
Плюсовое значение математической вероятности указывает, что при большом количестве ставок при верном прогнозе игрок получит прибыль.
Вывод
Без математики в ставках на спорт делать нечего. Играть ради развлечения, проигрывая маленькие суммы – это, пожалуйста, но если беттор собирается в долгосрочной перспективе получить прибыль и обыгрывать букмекерские конторы, математика в ставках ему будет просто необходима, и игнорировать ее не получится.
 comments powered by HyperComments
comments powered by HyperCommentsbukmekery-online.ru










